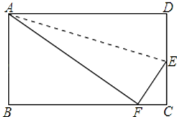
题目内容
【题目】![]() 、
、![]() 、
、![]() 、
、![]() 为矩形的四个顶点,
为矩形的四个顶点,![]() ,
,![]() ,动点
,动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,点
同时出发,点![]() 以
以![]() 的速度向点
的速度向点![]() 移动,一直到达
移动,一直到达![]() 为止,点
为止,点![]() 以
以![]() 的速度向
的速度向![]() 移动.
移动.

(1)![]() 、
、![]() 两点从出发开始到几秒时四边形
两点从出发开始到几秒时四边形![]() 是矩形?
是矩形?
(2)![]() 、
、![]() 两点从出发开始到几秒时,点
两点从出发开始到几秒时,点![]() 和点
和点![]() 的距离是
的距离是![]() ?
?
【答案】(1)当![]() 、
、![]() 两点从出发开始到
两点从出发开始到![]() 秒时四边形
秒时四边形![]() 是矩形秒时四边形
是矩形秒时四边形![]() 为矩形;
为矩形;![]() ,
,![]() 两点从出发开始到
两点从出发开始到![]() 或
或![]() 秒时,点
秒时,点![]() ,
,![]() 间的距离是
间的距离是![]() .
.
【解析】
(1)当PB=CQ时,四边形PBCQ为矩形,依此建立方程求出即可;
(2)作PH⊥CD,垂足为H,设运动时间为t秒,用t表示线段长,用勾股定理列方程求解.
(1)如图,∵A、B、C、D为矩形的四个顶点,
∴∠B=90°,AB∥CD,
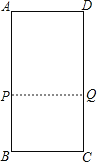
∴当PB=CQ时,四边形PBCQ为矩形,
设P、Q两点从出发开始到t秒时四边形PBCQ是矩形,
则16-3t=2t,
解得:t=![]() .
.
答:当![]() 、
、![]() 两点从出发开始到
两点从出发开始到![]() 秒时四边形
秒时四边形![]() 是矩形秒时四边形
是矩形秒时四边形![]() 为矩形;
为矩形;
![]() 设
设![]() ,
,![]() 两点从出发开始到
两点从出发开始到![]() 秒时,点
秒时,点![]() ,
,![]() 间的距离是
间的距离是![]() ,
,
作![]() ,垂足为
,垂足为![]() ,则
,则![]() ,
,![]() ,
,

∵![]() ,
,![]() ,
,
∴![]() ,
,
由勾股定理,得![]() ,
,
解得![]() ,
,![]() .
.
答:![]() ,
,![]() 两点从出发开始到
两点从出发开始到![]() 或
或![]() 秒时,点
秒时,点![]() ,
,![]() 间的距离是
间的距离是![]() .
.

练习册系列答案
相关题目