题目内容
【题目】如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动.若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求: 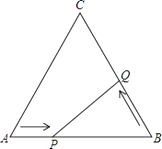
(1)经过6秒后,BP=cm,BQ=cm;
(2)经过几秒后,△BPQ是直角三角形?
(3)经过几秒△BPQ的面积等于 ![]() cm2?
cm2?
【答案】
(1)6;12
(2)解:∵△ABC是等边三角形,
∴AB=BC=12cm,∠A=∠B=∠C=60°,
当∠PQB=90°时,
∴∠BPQ=30°,
∴BP=2BQ.
∵BP=12﹣x,BQ=2x,
∴12﹣x=2×2x,
∴x= ![]() ,
,
当∠QPB=90°时,
∴∠PQB=30°,
∴BQ=2PB,
∴2x=2(12﹣x),
x=6
答6秒或 ![]() 秒时,△BPQ是直角三角形
秒时,△BPQ是直角三角形
(3)解:作QD⊥AB于D,
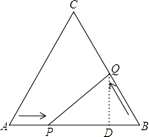
∴∠QDB=90°,
∴∠DQB=30°,
∴DB= ![]() BQ=x,
BQ=x,
在Rt△DBQ中,由勾股定理,得
DQ= ![]() x,
x,
∴ ![]() ,
,
解得;x1=10,x2=2,
∵x=10时,2x>12,故舍去
∴x=2.
答:经过2秒△BPQ的面积等于 ![]() cm2.
cm2.
【解析】解:(1)由题意,得 AP=6cm,BQ=12cm.
∵△ABC是等边三角形,
∴AB=BC=12cm,
∴BP=12﹣6=6cm.
故答案为:6、12.
(1)根据路程=速度×时间,求出BQ,AP的值就可以得出结论;(2)先分别表示出BP,BQ的值,当∠BQP和∠BPQ分别为直角时,由等边三角形的性质就可以求出结论;(3)作QD⊥AB于D,由勾股定理可以表示出DQ,然后根据面积公式建立方程求出其解即可.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目