Question

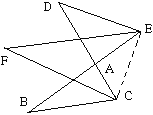
【题目】如图，BE，CD相交于点A，∠DEA、∠BCA的平分线相交于F.

（1）探求：∠F与∠B、∠D有何等量关系？

（2）当∠B︰∠D︰∠F=2︰4︰x时，x为多少？

Answer 1

【答案】【答案:（1）∠F=（∠B+∠D）；（2）3.

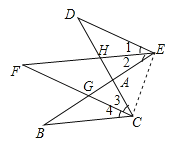
【解析】试题分析：（1）由三角形内角和外角的关系可知∠D+∠1=∠3+∠F，∠2+∠F=∠B+∠4，由角平分线的性质可知∠1=∠2，∠3=∠4，故∠F=（∠B+∠D）．

（2）设∠B=2α，则∠D=4α．利用（1）中的结论和已知条件来求x的值．

试题解析：解：（1）∠F=（∠B+∠D）；

理由如下：

∵∠DHF是△DEH的外角，∠EHC是△FCH的外角，∠DHF=∠EHC，∴∠D+∠1=∠3+∠F ①

同理，∠2+∠F=∠B+∠4 ②

又∵∠DEA，∠BCA的平分线相交于F，∴∠1=∠2，∠3=∠4；

∴①﹣②得：∠B+∠D=2∠F，即∠F=（∠B+∠D）．

（2）∵∠B：∠D：∠F=2：4：x，∴设∠B=2α，则∠D=4α，∴∠F=（∠B+∠D）=3α，又∠B：∠D：∠F=2：4：x，∴x=3．