题目内容
【题目】如图,已知二次函数y=ax2+bx+8(a≠0)的图象与x轴交于点A(﹣2,0),
B(4,0)与y轴交于点C.
(Ⅰ)求抛物线的解析式及其顶点D的坐标;
(Ⅱ)求△BCD的面积;
(Ⅲ)若直线CD交x轴与点E,过点B作x轴的垂线,交直线CD与点F,将抛物线沿其对称轴向上平移,使抛物线与线段EF总有公共点.试探究抛物线最多可以向上平移多少个单位长度(直接写出结果,不写求解过程).

【答案】(Ⅰ)抛物线的解析式:y=﹣x2+2x+8=﹣(x﹣1)2+9,顶点D(1,9);(Ⅱ)6;(Ⅲ)72.
【解析】
试题分析:(Ⅰ)利用待定系数法求出抛物线的解析式,通过对解析式进行配方能得到顶点D的坐标;
(Ⅱ)先求出直线BC解析式,进而用三角形的面积公式即可得出结论.
(Ⅲ)首先确定直线CD的解析式以及点E,F的坐标,若抛物线向上平移,首先表示出平移后的函数解析式;当x=﹣8时(与点E横坐标相同),求出新函数的函数值,若抛物线与线段EF有公共点,那么该函数值应不大于点E的纵坐标.当x=4时(与点F的横坐标相同),方法同上,结合上述两种情况,即可得到函数图象的最大平移单位.
试题解析:(Ⅰ)将A、B的坐标代入抛物线的解析式中,得:
![]() ,解得
,解得![]() ,
,
∴抛物线的解析式:y=﹣x2+2x+8=﹣(x﹣1)2+9,顶点D(1,9);
(Ⅱ)如图1,
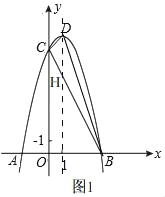
∵抛物线的解析式:y=﹣x2+2x+8,
∴C(0,8),
∵B(4,0),
∴直线BC解析式为y=﹣2x+8,
∴直线和抛物线对称轴的交点H(1,6),
∴S△BDC=S△BDH+S△DHC=![]() ×3×1+
×3×1+![]() ×3×3=6.
×3×3=6.
(Ⅲ)如图2,
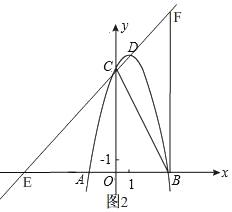
∵C(0,8),D(1,9);
代入直线解析式y=kx+b,
∴![]() ,
,
解得:![]() ,
,
∴y=x+8,
∴E点坐标为:(﹣8,0),
∵B(4,0),
∴x=4时,y=4+8=12
∴F点坐标为:(4,12),
设抛物线向上平移m个单位长度(m>0),
则抛物线的解析式为:y=﹣(x﹣1)2+9+m;
当x=﹣8时,y=m﹣72,
当x=4时,y=m,
∴m﹣72≤0 或 m≤12,
∴0<m≤72,
∴抛物线最多向上平移72个单位.