��Ŀ����
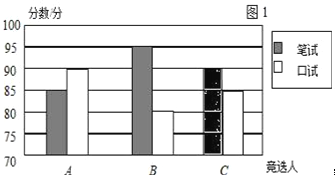
����Ŀ��������ѧ����ѡϵѧ������ϯ�����ǵı��Գɼ��Ϳ��Գɼ�����λ���֣��ֱ��������ַ�ʽ������ͳ�ƣ����һ��ͼһ��
��1���뽫��һ��ͼһ�еĿ�ȱ���ֲ���������
��2����ѡ�����һ���������ɱ�ϵ��300��ѧ������ͶƱ����λ��ѡ�˵ĵ�Ʊ�����ͼ����û����ȨƱ��ÿ��ѧ��ֻ���Ƽ�һ�����������ÿ�˵ĵ�Ʊ����
��3����ÿƱ��1�֣�ϵ�ォ���ԡ����ԡ���Ʊ������Ե÷ְ�![]() �ı���ȷ�����˳ɼ����������λ��ѡ�˵����ɼ��������ݳɼ��ж�˭�ܵ�ѡ��
�ı���ȷ�����˳ɼ����������λ��ѡ�˵����ɼ��������ݳɼ��ж�˭�ܵ�ѡ��

���𰸡�(1)��ͼ����������2��A,105;B,120;C,75;(3)B.
�������������������1������ͳ��ͼ�ɵ�A�Ŀ��Գɼ���90������ͳ�Ʊ��ɵ�C�ı��Գɼ���90�֣�������ͼ��
��2������B��ռ�ı�������360�ȼ�����⣻
��3���������A��B��C��ͶƱ�÷֣�Ȼ�����ü�Ȩƽ������ʽ������⣮
�����������1������ͼ�����£�
��ѡ�� | A | B | C |
���� | 85 | 95 | 90 |
���� | 90 | 80 | 85 |
 ��
��
��2��360���40%=144����
�ʴ�Ϊ��144����
��3��A��ͶƱ�÷��ǣ�300��35%=105���֣�����A�����÷���![]() =92.5���֣���
=92.5���֣���
B��ͶƱ�õ��ǣ�300��40%=120���֣�����B�����÷���![]() =98���֣���
=98���֣���
C��ͶƱ�÷��ǣ�300��25%=75���֣�����C�����յ÷���![]() =84���֣���
=84���֣���
����B��ѡ��

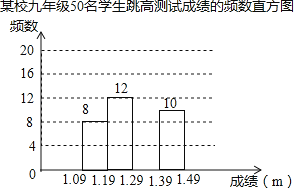
����Ŀ��Ϊ���˽�ijУ���꼶ѧ��������ˮƽ�������ȡ���꼶50��ѧ���������߲��ԣ����Ѳ��Գɼ����Ƴ���ͼ��ʾ��Ƶ������δ��ɵ�Ƶ��ֱ��ͼ��ÿ�麬ǰһ���߽�ֵ��������һ���߽�ֵ����
ijУ���꼶50��ѧ�����߲��Գɼ���Ƶ����
���m�� | Ƶ�� |
1.09��1.19 | 8 |
1.19��1.29 | 12 |
1.29��1.39 | A |
1.39��1.49 | 10 |
��1����a��ֵ������Ƶ��ֱ��ͼ����������
��2�����꼶����500��ѧ�������Ƹ��꼶ѧ�����߳ɼ���1.29m����1.29m�����ϵ�������
����Ŀ����ˮ��ƽ�����Ϊ2.5�ף�һ������1.5��������Ӿ������ˮ�� ��
A.�϶�������B.��һ��������C.�Ͳ���D.���ϴ𰸶�����
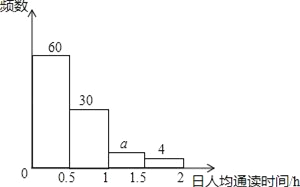
����Ŀ��ijУ1200��ѧ���μ���ȫ����֯���������ж��������У���ѡȡ����ѧ�����������������������µ��ж�ʱ����е��飬�����Ǹ��ݵ�������������ͳ��ͼ����һ���֣�
����������Ϣ������������⣺
��1�����ε����ѧ����Ϊ__�ˣ�
��2��ͼ���е�a��b��c��ֵ�ֱ�Ϊ__��__��__��
��3���ڱ������ѧ���У����·����˾��ж�ʱ����1��x��1.5��Χ�ڵ����������·��ڴ˷�Χ��������__�ˣ�
��4���Թ��Ƹ�Уѧ�����·��˾��ж�ʱ����1Сʱ���ϵ�������
�������˾��ж�ʱ���ͳ�Ʊ�
���˾��ж�ʱ��x/h | ���� | �ٷֱ� |
0��x��0.5 | 6 | |
0.5��x��1 | 30 | |
1��x��1.5 | 50% | |
1.5��x��2 | 10 | 10% |
2��x��2.5 | b | c |
�������˾��ж�ʱ���Ƶ���ֲ�ֱ��ͼ