题目内容
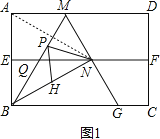
【题目】如图，四边形ABCD是矩形纸片，
对折矩形纸片ABCD，使AD与BC重合折痕为EF；展平后再过点B折叠矩形纸片，使点A落在EF上的点N，折痕BM与EF相交于点Q；再次展平，连接BN，MN，延长MN交BC于点
有如下结论：
；
是等边三角形；
；
为线段BM上一动点，H是BN的中点，则
的最小值是
其中正确结论的个数是
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】
首先根据EF垂直平分AB，可得
；然后根据折叠的性质，可得
，据此判断出
为等边三角形，即可判断出
求出
；然后在
中，根据
，求出AM的大小即可．
根据对折得
，再由平行线的性质和三角形的内角和定理得：
，即可推得
是等边三角形．
根据平行线等分线段定理得：
，
，得QN是的中位线，可得QN的长；
首先根据是等边三角形，点N是MG的中点，判断出
，即可求出BN的大小；然后根据E点和H点关于BM称可得
，因此P与Q重合时，
，据此求出
的最小值是多少即可．
如图1，连接AN，交BM于P，
垂直平分AB，
，
根据折叠的性质，可得，
．
为等边三角形．
，
，
，
故不正确；
，
，
，
，
为等边三角形，
故正确；
由知：为等边三角形，
，
，
，
，，
是的中位线，
，
故不正确．
是等边三角形，点N是MG的中点，
，
，
根据条件易知E点和H点关于BM对称，
，
与Q重合时，的值最小，此时，如图2，
，
的最小值是
，
故正确．
本题结论正确的有：
，2个，
故选：B．
练习册系列答案
阅读快车系列答案
相关题目
