题目内容
【题目】如图,一艘轮船位于灯塔B的正西方向A处,且A处与灯塔B相距60海里,轮船沿东北方向匀速航行,到达位于灯塔B的北偏东l5°方向上的C处.

(1)求∠ACB的度数;
(2)求灯塔B到C处的距离.(结果保留根号)
【答案】(1)30°;(2)60![]() 海里.
海里.
【解析】
(1)利用三角形内角和定理进行计算;
(2)过点B作AC的垂线,垂足为D.在△BDC中利用三角函数即可求解.
(1)在△ABC中,∠CAB=45°,∠CBA=90°+15°=105°.则∠ACB=180°-45°-105°=30°,即∠ACB=30°;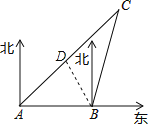
(2)过点B作AC的垂线,垂足为D,依题意可得∠DAB=45°,∠DBA=45°,AB=60海里.
AD=BD=ABsin45=60×![]() .
.
在△BDC中,∠DBC=45°+15°=60°,∠BDC=90°,cos∠DBC=![]() =cos60°=
=cos60°=![]() .
.
∴BC=60![]() (海里).
(海里).
答:灯塔B到C处的距离是60![]() 海里.
海里.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目







