题目内容
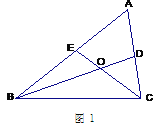
【题目】(1)如图1,在△ABC中∠A=60 ,BD、CE均为△ABC的角平分线且相交于点O.
①填空:∠BOC= 度;
②求证:BC=BE+CD.(写出求证过程)
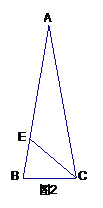
(2)如图2,在△ABC中,AB=AC=m,BC=n, CE平分∠ACB.
①若△ABC的面积为S,在线段CE上找一点M,在线段AC上找一点N,使得AM+MN的值最小,则AM+MN的最小值是 .(直接写出答案);
②若∠A=20°,则△BCE的周长等于 .(直接写出答案).
【答案】(1)①120;②证明见解析;(2)①![]() (或
(或![]() );②m
);②m
【解析】试题分析:(1)①根据三角形内角和定理得到∠BOC=180°-∠OBC-∠OCB,则2∠BOC=360°-2∠OBC-2∠OCB,再根据角平分线的定义得∠ABC=2∠OBC,∠ACB=2∠OCB,则2∠BOC=360°-∠ABC-∠ACB,易得∠BOC=90°+![]() ∠A,由∠A=60 即可得∠BOC的值;
∠A,由∠A=60 即可得∠BOC的值;
②采用截长法在在BC上截取BF=BE,连接OF,由边角边证得△EBO≌△FBO,再由角边角证得△DCO≌△FCO,即可得证;
(2)①当AM⊥BC时,AM+MN的值最小;
②在CA上截取CD=CB,以E为圆心EC为半径画弧,与AC交于点F,通过构造全等三角形,利用等腰三角形的判定和性质即可求解.
试题解析:(1)①在△OBC中,∠BOC=180°-∠OBC-∠OCB,
∴2∠BOC=360°-2∠OBC-2∠OCB,
∵BD、CE均为△ABC的角平分线,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴2∠BOC=360°-∠ABC-∠ACB,
∴∠BOC=90°+![]() ∠A,
∠A,
∵∠A=60 ,
∴∠BOC=90°+![]() ×60 =120°;
×60 =120°;
故答案为:120°;
②证明:由(1)①∠BOC=120°,
∴∠BOE=∠COD=180°-120°=60°,
在BC上截取BF=BE,连接OF,

∵BD平分∠ABC,
∴∠EBO=∠FBO,
又∵BO=BO(公共边相等)
∴△EBO≌△FBO(SAS)
∴∠BOF=∠BOE=60°,
∴∠COF=∠BOC-∠BOF=120°-60°=60°=∠COD,
∵CE平分∠ACB,
∴∠DCO=∠FCO,
又∵CO=CO(公共边相等)
∴△DCO≌△FCO(ASA)
∴CD=CF,
∴BC=BF+CF=BE+CD;
(2)①如图:

当AM⊥BC时,与BC交于点D,过M作MN⊥AC交AC与点D,
∵CE平分∠ACB,
∴DM=DN,
∴AD=AM+MD=AM+MN,
此时,AM+MN的值最小,
由S△ABC=![]() BC·AD,BC=n,△ABC的面积为S,
BC·AD,BC=n,△ABC的面积为S,
得AD=![]() ,
,
或∵AB=AC, AD⊥BC, AB=AC=m,BC=n,
∴BD=CD=![]() ,
,
在Rt△ACD中,由勾股定理得AD=![]() ;
;
故答案为: ![]() (或
(或![]() );
);
②如图:在CA上截取CD=CB,以E为圆心EC为半径画弧,与AC交于点F,

∵AB=AC=m,∠A=20°,
∴∠B=∠C=80°,
∵CE平分∠ACB,
∴∠BCE=∠DCE=40°,
∵CE=CE,
∴△BCE≌△DCE,
∴∠CDE=∠B=80°,∠DEC=∠BEC=60°,BE=DE,
∴∠CDE=40°,
∵EC=EF,
∴∠EFC=∠ECF=40°,
∴∠DEF=∠CDE-∠DFE=40°,
∴DE=DF,
∠AEF=∠DFE-∠A=40°-20°=20°,
∴EF=AF,
∴BE=DF,CE=AF,
∴△BCE的周长=BC+CE+BE=CD+AF+DF=AC=m.

 名校课堂系列答案
名校课堂系列答案