题目内容
(2013•鹰潭模拟)某校九年级(1)班数学兴趣小组开展了一次活动,过程如下:
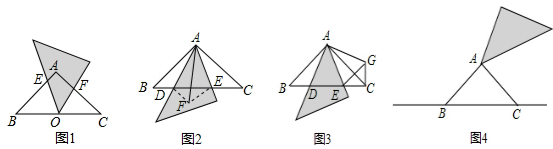
如图1,在等腰直角△ABC中,AB=AC,∠BAC=90°,小明将一块直角三角板的直角顶点放在斜边BC边的中点O上,从BC边开始绕点A顺时针旋转,其中三角板两条直角边所在的直线分别交AB、AC于点E、F.
(1)小明在旋转中发现:在图1中,线段AE与CF相等.请你证明小明发现的结论;
(2)小明将一块三角板中含45°角的顶点放在点A上,从BC边开始绕点A顺时针旋转一个角α,其中三角板斜边所在的直线交直线BC于点D,直角边所在的直线交直线BC于点E.当0°<α≤45°时,小明在旋转中还发现线段BD、CE、DE之间存在如下等量关系:
BD2+CE2=DE2.同组的小颖和小亮随后想出了两种不同的方法进行解决:
小颖的方法:将△ABD沿AD所在的直线对折得到△ADF,连接EF(如图2);
小亮的方法:将△ABD绕点A逆时针旋转90°得到△ACG,连接EG(如图3).
请你从中任选一种方法进行证明;
(3)小明继续旋转三角板,在探究中得出:当45°<α<135°且α≠90°时,等量关系BD2+CE2=DE2仍然成立.现请你继续探究:当135°<α<180°时(如图4),等量关系BD2+CE2=DE2是否仍然成立?若成立,给出证明;若不成立,说明理由.
如图1,在等腰直角△ABC中,AB=AC,∠BAC=90°,小明将一块直角三角板的直角顶点放在斜边BC边的中点O上,从BC边开始绕点A顺时针旋转,其中三角板两条直角边所在的直线分别交AB、AC于点E、F.
(1)小明在旋转中发现:在图1中,线段AE与CF相等.请你证明小明发现的结论;
(2)小明将一块三角板中含45°角的顶点放在点A上,从BC边开始绕点A顺时针旋转一个角α,其中三角板斜边所在的直线交直线BC于点D,直角边所在的直线交直线BC于点E.当0°<α≤45°时,小明在旋转中还发现线段BD、CE、DE之间存在如下等量关系:
BD2+CE2=DE2.同组的小颖和小亮随后想出了两种不同的方法进行解决:
小颖的方法:将△ABD沿AD所在的直线对折得到△ADF,连接EF(如图2);
小亮的方法:将△ABD绕点A逆时针旋转90°得到△ACG,连接EG(如图3).
请你从中任选一种方法进行证明;
(3)小明继续旋转三角板,在探究中得出:当45°<α<135°且α≠90°时,等量关系BD2+CE2=DE2仍然成立.现请你继续探究:当135°<α<180°时(如图4),等量关系BD2+CE2=DE2是否仍然成立?若成立,给出证明;若不成立,说明理由.

分析:(1)连接OA,证△AEO≌△CFO,推出AE=CF即可;
(2)成立.小颖的方法是应用折叠对称的性质和SAS得到△AEF≌△AEC,在Rt△DFE中应用勾股定理而证明;小亮的方法是将△ABD绕点A逆时针旋转90°得到△ACG,根据旋转的性质用SAS得到△ACE≌△ACG,从而在Rt△CEG中应用勾股定理而证明.
(3)当135°<α<180°时,等量关系BD2+CE2=DE2仍然成立.可以根据小颖和小亮的方法进行证明即可.
(2)成立.小颖的方法是应用折叠对称的性质和SAS得到△AEF≌△AEC,在Rt△DFE中应用勾股定理而证明;小亮的方法是将△ABD绕点A逆时针旋转90°得到△ACG,根据旋转的性质用SAS得到△ACE≌△ACG,从而在Rt△CEG中应用勾股定理而证明.
(3)当135°<α<180°时,等量关系BD2+CE2=DE2仍然成立.可以根据小颖和小亮的方法进行证明即可.
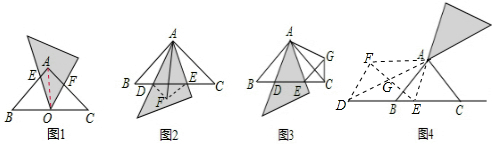
解答:(1)证明:如图1,连接OA.
∵在等腰直角△ABC中,AB=AC,∠BAC=90°,
∴∠B=∠C=45°.
又∵点O是BC的中点,
∴OA=OC,∠EAO=∠C=45°.
∵∠EOF=90°,
∴∠AEO=∠B+∠BOE,∠CFO=180°-∠C-(180°-∠BOE-90°)=45°+∠BOE=∠B+∠BOE,
∴∠AEO=CFO,
在△AEO与△CFO中,
,
∴△AEO≌△CFO(AAS),
∴AE=CF;
(2)选择小颖的方法.
证明:如图2,连接EF.
由折叠可知,∠BAD=∠FAD,AB=AF,BD=DF,
∵∠BAD=∠FAD,
∴由(1)可知,∠CAE=∠FAE.
在△AEF和△AEC中,
,
∴△AEF≌△AEC(SAS),
∴CE=FE,∠AFE=∠C=45°.
∴∠DFE=∠AFD+∠AFE=90°.
在Rt△DFE中,DF2+FE2=DE2,
∴BD2+CE2=DE2.
(3)解:当135°<α<180°时,等量关系BD2+CE2=DE2仍然成立.证明如下:
如图4,按小颖的方法作图,设AB与EF相交于点G.
∵将△ABD沿AD所在的直线对折得到△ADF,
∴AF=AB,∠AFD=∠ABD=135°,∠BAD=∠FAD.
又∵AC=AB,∴AF=AC.
又∵∠CAE=90°-∠BAE=90°-(45°-∠BAD)=45°+∠BAD=45°+∠FAD=∠FAE.
∴∠CAE=∠FAE.
在△AEF和△AEC中,
,
∴△AEF≌△AEC(SAS),
∴CE=FE,∠AFE=∠C=45°.
∴∠DFE=∠AFD-∠AFE=∠135°-∠C=135°-45°=90°.
∴∠DFE=90°.
在Rt△DFE中,DF2+FE2=DE2,∴BD2+CE2=DE2.
∵在等腰直角△ABC中,AB=AC,∠BAC=90°,
∴∠B=∠C=45°.
又∵点O是BC的中点,
∴OA=OC,∠EAO=∠C=45°.
∵∠EOF=90°,
∴∠AEO=∠B+∠BOE,∠CFO=180°-∠C-(180°-∠BOE-90°)=45°+∠BOE=∠B+∠BOE,
∴∠AEO=CFO,
在△AEO与△CFO中,
|
∴△AEO≌△CFO(AAS),
∴AE=CF;
(2)选择小颖的方法.
证明:如图2,连接EF.
由折叠可知,∠BAD=∠FAD,AB=AF,BD=DF,
∵∠BAD=∠FAD,
∴由(1)可知,∠CAE=∠FAE.
在△AEF和△AEC中,
|
∴△AEF≌△AEC(SAS),
∴CE=FE,∠AFE=∠C=45°.
∴∠DFE=∠AFD+∠AFE=90°.
在Rt△DFE中,DF2+FE2=DE2,
∴BD2+CE2=DE2.
(3)解:当135°<α<180°时,等量关系BD2+CE2=DE2仍然成立.证明如下:
如图4,按小颖的方法作图,设AB与EF相交于点G.
∵将△ABD沿AD所在的直线对折得到△ADF,
∴AF=AB,∠AFD=∠ABD=135°,∠BAD=∠FAD.
又∵AC=AB,∴AF=AC.
又∵∠CAE=90°-∠BAE=90°-(45°-∠BAD)=45°+∠BAD=45°+∠FAD=∠FAE.
∴∠CAE=∠FAE.
在△AEF和△AEC中,
|
∴△AEF≌△AEC(SAS),
∴CE=FE,∠AFE=∠C=45°.
∴∠DFE=∠AFD-∠AFE=∠135°-∠C=135°-45°=90°.
∴∠DFE=90°.
在Rt△DFE中,DF2+FE2=DE2,∴BD2+CE2=DE2.

点评:本题考查了角平分线的定义,等腰直角三角形的性质,旋转的性质,折叠对称的性质,全等三角形的判定和性质等知识点.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 (2013•鹰潭模拟)在平行四边形ABCD中,点E是DC上一点,且CE=BC,AB=8,BC=5.
(2013•鹰潭模拟)在平行四边形ABCD中,点E是DC上一点,且CE=BC,AB=8,BC=5.
 (2013•鹰潭模拟)如图是跷跷板示意图,横板AB绕中点O上下转动,立柱OC与地面垂直,跷跷板AB的一端B碰到地面时,AB与地面的夹角为15°,且AB=6m.
(2013•鹰潭模拟)如图是跷跷板示意图,横板AB绕中点O上下转动,立柱OC与地面垂直,跷跷板AB的一端B碰到地面时,AB与地面的夹角为15°,且AB=6m. (2013•鹰潭模拟)如图,AB是⊙O的直径,AC是弦,∠ACD=
(2013•鹰潭模拟)如图,AB是⊙O的直径,AC是弦,∠ACD=