题目内容
 (2013•鹰潭模拟)在平行四边形ABCD中,点E是DC上一点,且CE=BC,AB=8,BC=5.
(2013•鹰潭模拟)在平行四边形ABCD中,点E是DC上一点,且CE=BC,AB=8,BC=5.(1)作AF平分∠BAD交DC于F(尺规作图,保留作图痕迹);
(2)在(1)的条件下求EF的长度.
分析:(1)根据角平分线画法:以A为圆心,以任意长为比较画弧,交AD和AB于点,再分别以这两点为圆心,以大于两点之间的距离为半径画弧,相交于一点,作射线即可;(2)求出DF=AD,CE=BC,代入EF=DF+CE-DC求出即可.
解答:解:(1)作图: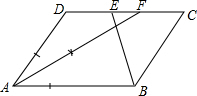
(2)∵AF平分∠BAD,∴∠DAF=∠BAF,∵AB∥DC,∴∠DFA=∠BAF,∴∠DAF=∠AFD,∴AD=DF,∵AD=BC,CE=BC=5,DC=AB=8,∴BF=CE=5,∴EF=DF+CE-DC=5+5-8=2,

(2)∵AF平分∠BAD,∴∠DAF=∠BAF,∵AB∥DC,∴∠DFA=∠BAF,∴∠DAF=∠AFD,∴AD=DF,∵AD=BC,CE=BC=5,DC=AB=8,∴BF=CE=5,∴EF=DF+CE-DC=5+5-8=2,
点评:本题考查了平行线性质,平行四边形的性质,等腰三角形的性质的应用,主要考查学生的画图能力和计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 (2013•鹰潭模拟)如图是跷跷板示意图,横板AB绕中点O上下转动,立柱OC与地面垂直,跷跷板AB的一端B碰到地面时,AB与地面的夹角为15°,且AB=6m.
(2013•鹰潭模拟)如图是跷跷板示意图,横板AB绕中点O上下转动,立柱OC与地面垂直,跷跷板AB的一端B碰到地面时,AB与地面的夹角为15°,且AB=6m. (2013•鹰潭模拟)如图,AB是⊙O的直径,AC是弦,∠ACD=
(2013•鹰潭模拟)如图,AB是⊙O的直径,AC是弦,∠ACD=