Question

如图，⊙O的直径CD垂直于弦AB，垂足为E，F为DC延长线上一点，且∠CBF=∠CDB．
（1）求证：FB为⊙O的切线；
（2）若AB=8，CE=2，求sin∠F．

Answer 1

（1）见解析；（2）

解析试题分析：（1）连接OB，由圆周角定理可得∠CBD=90°，再由圆所具有的性质及已知条件，可得∠OBF=90°；从而问题得证；
（2）先由垂径定理求得BE的长，然后根据△OBE∽△OBF，利用相似三角形的性质求得OF的长，则sinF即可求解．
试题解析：（1）连接OB．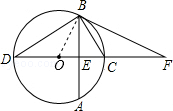

∵CD是直径，
∴∠CBD=90°，
又∵OB=OD，
∴∠OBD=∠D，
又∠CBF=∠D，
∴∠CBF=∠OBD，
∴∠OBF=90°，即OB⊥BF，
∴FB是圆的切线；
（2）∵CD是圆的直径，CD⊥AB，
∴BE=AB=4，
设圆的半径是R，在直角△OEB中，根据勾股定理得：R²=（R﹣2）²+4²，
解得：R=5，
∵∠BOE=∠FOB，∠BEO=∠OBF，
∴△OBE∽△OBF，
∴OB²=OE•OF，
∴OF=，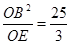
则在直角△OBF中，sinF=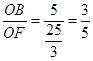
考点：1、圆周角定理；2、切线的判定；3、相似三角形的判定与性质；4、勾股定理