题目内容
【题目】”4.20芦山地震”发生后，各地积极展开抗震救援工作，一支救援车队经过如图1所示的一座拱桥，拱桥的轮廓是抛物线型，拱高6m，跨度20m，相邻两支柱间的距离均为5m，将抛物线放在所给的直角坐标系中（如图2所示），拱桥的拱顶在y轴上．
（1）求拱桥所在抛物线的解析式；
（2）求支柱MN的长度；
（3）拱桥下地平面是双向行车道（正中间是一条宽2米的隔离带），其中的一条行车道能否并排行驶宽2m、高2.4m的三辆汽车（隔离带与内侧汽车的间隔、汽车间的间隔、外侧汽车与拱桥的间隔均为0.5m）？请说说你的理由．
【答案】解：（1）根据题目条件，A、B、C的坐标分别是（﹣10，0）、（10，0）、（0，6）．
将B、C的坐标代入y=ax2+c，得
解得a=﹣
，c=6．
所以抛物线的表达式是y=﹣x2+6；
（2）可设N（5，yN），于是yN=﹣×52+6=4.5．
从而支柱MN的长度是10﹣4.5=5.5米；
（3）设DE是隔离带的宽，EG是三辆车最内侧与最外侧的宽度和，则G点坐标是（9，0），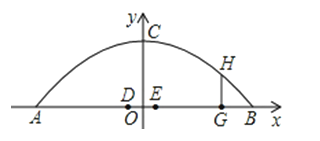
过G点作GH垂直AB交抛物线于H，则yH=﹣×92+6=1.14＜2.4，
根据抛物线的特点，可知一条行车道不能并排行驶这样的三辆汽车．
【解析】（1）根据题目可知A．B，C的坐标，设出抛物线的解析式代入可求解；
（2）设N点的坐标为（5，yN）可求出支柱MN的长度；
（3）设DE是隔离带的宽，EG是三辆车的宽度和，作GH垂直AB交抛物线于H，求出GH则可求解．
练习册系列答案
相关题目
