Question

【题目】如图1，已知：直线y=x﹣3分别交x轴于A，交y轴于B，抛物线C1：y=x2+4x+b的顶点D在直线AB上．
（1）求抛物线C1的解析式；
（2）如图2，将抛物线C1的顶点沿射线DA的方向平移得抛物线C2 ， 抛物线C2交y轴于C，顶点为E，若CE⊥AB，求抛物线C2的解析式；
（3）如图3，将直线AB沿y轴正方向平移t（t＞0）个单位得直线l，抛物线C1的顶点在直线AB上平移得抛物线C3 ， 直线l和抛物线C3相交于P、Q，求当t为何值时，PQ=3？

Answer 1

【答案】解：（1）由y=x2+4x+b=（x+2）2﹣4+b，
∴顶点D的坐标（﹣2，﹣4+b），
代入y=x﹣3得：﹣4+b=×（﹣2）﹣3，
解得：b=0，
∴抛物线C1的解析式为：y=x2+4x；
（2）∵抛物线C1的顶点沿射线DA的方向平移得抛物线C2 ，
∴抛物线C1的向右平移a个单位的同时向上平移a个单位，
∵y=x2+4x=（x+2）2﹣4，
∴抛物线C2的解析式为：y=（x+2﹣a）2﹣4+，
∴E（﹣2+a，﹣4+），
令x=0，则y=a2﹣a，
∵CE⊥AB，
∴直线CE的斜率为﹣2，
∴直线CE为：y=﹣2x+a2﹣a，
∴﹣4+=﹣2（﹣2+a）+a2﹣a，
解得：a=2（舍去），a=4，
∴抛物线C2的解析式为：y=（x﹣2）2﹣2；
（3）∵PQ的长与C3移动到的位置无关，
∴当抛物线C3的顶点在y轴时，抛物线的解析式为：y=x2﹣3，
∵直线AB沿y轴正方向平移t（t＞0）个单位得直线l，
∴直线l的解析式为：y=x﹣3+t，
解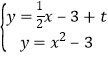，得：x1=，x2=，
∵x1﹣x2=，
∴PQ2=（）2+（）2=，
∵PQ=3，
∴PQ2=45，
∴=45，
解得t=，
∴当t=时，P、Q之间的距离为3．
【解析】（1）根据抛物线的解析式转化为顶点式，求得顶点D的坐标，把D的坐标代入，直线的解析式即可求得b的值进而求得抛物线C1的解析式；
（2）先得出抛物线C2的解析式为：y=（x+2﹣a）2﹣4+ ， 求得顶点E的坐标，令x=0，求得y=a2﹣a，由于CE⊥AB，所以直线CE的斜率为﹣2，进而求得直线CE为：y=﹣2x+a2﹣a，把顶点的坐标代入即可求得a的值，从而求得抛物线C2的解析式；
（3）PQ的长与C3移动到的位置无关，当抛物线C3的顶点在y轴时，抛物线的解析式为：y=x2﹣3，先求得直线l的解析式，然后与抛物线y=x2﹣3组成方程组，解方程组即可求得P、Q的横坐标，根据直线的斜率求得纵坐标的差等于横坐标差的一半，根据勾股定理即可求得PQ2 ， 与已知条件PQ=3列出等式即可求得t的值；