题目内容
【题目】探索:小明在研究数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠C的数量关系.

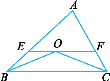
发现:在如图中,:∠APC=∠A+∠C;如图
小明是这样证明的:过点P作PQ∥AB
∴∠APQ=∠A(_ __)
∵PQ∥AB,AB∥CD.
∴PQ∥CD(__ _)
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
(1)为小明的证明填上推理的依据;
(2)应用:①在如图中,∠P与∠A、∠C的数量关系为__ _;
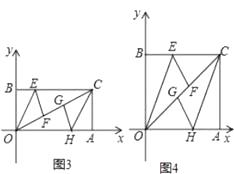
②在如图中,若∠A=30![]() ,∠C=70
,∠C=70![]() ,则∠P的度数为__ _;
,则∠P的度数为__ _;
(3)拓展:在如图中,探究∠P与∠A,∠C的数量关系,并说明理由.
【答案】(1)两直线平行,内错角相等;平行于同一直线的两直线平行;(2)∠APC+∠A+∠C=360;40°;(3)![]()
【解析】
(1)过点P作PQ∥AB,根据平行线的性质得出∠APQ=∠A,∠CPQ=∠C,即可得出答案;
(2)①过点P作PQ∥AB,根据平行线的性质得出∠APQ+∠A=180°,∠CPQ+∠C=180°,即可得出答案;
②根据平行线的性质得出∠PEB=∠C=70°,根据三角形外角性质得出即可;
(3)根据平行线的性质得出∠APG+∠A=180°,求出∠APG=180°-∠A,根据PG∥CD得出∠CPG+∠C=180°,即可得出答案.
(1)证明:过点P作PQ∥AB,
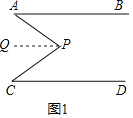
所以∠APQ=∠A(两直线平行,内错角相等)
∵PQ∥AB,AB∥CD.
∴PQ∥CD(平行于同一直线的两直线平行)
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
故答案为两直线平行,内错角相等;平行于同一直线的两直线平行;
(2)①
解:过点P作PQ∥AB,
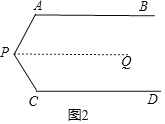
所以∠APQ+∠A=180°,
∵PQ∥AB,AB∥CD.
∴PQ∥CD,
∴∠CPQ+∠C=180°,
∴∠APQ+∠CPQ+∠A+∠C=360°,
即∠APC+∠A+∠C=360°,
故答案为∠APC+∠A+∠C=360°;
②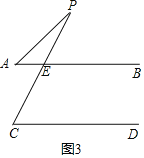
解:∵AB∥CD,∠C=70°,
∴∠PEB=∠C=70°,
∵∠A=30°,
∴∠P=∠PEB-∠A=40°,
故答案为40°;
(3)解:
∠APC=∠A-∠C.
理由是:如图4,过点P作PG∥AB,
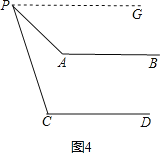
∵PG∥AB,
∴∠APG+∠A=180°,
∴∠APG=180°-∠A
∵PG∥AB,AB∥CD,
∴PG∥CD,(平行于同一直线的两直线平行)
∴∠CPG+∠C=180°,
∴∠CPG=180°-∠C,
∴∠APC=∠CPG-∠APG=∠A-∠C.