题目内容
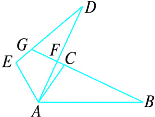
【题目】如图所示,△ ABC ≌△ ADE ,延长 BC 分别交 AD , DE 于 F , G ,∠ CAD =10°,∠ B =∠ D =25°,∠ EAB =120°.求∠ DFB 和∠ DGB 的度数.
【答案】 ∠ DFB =90°;∠ DGB=65°.
【解析】整体分析:
根据△ABC≌△ADE,∠CAD=10°,∠EAB=120°,求∠BAC,由三角形的外角等于和它不相邻的两个内角的和可求∠DFB,∠DGB.
解:∵△ABC≌△ADE,∴∠DAE=∠BAC.
∵∠CAD=10°,∠EAB=120°,
∴∠DAE=∠BAC=(120°-10°)÷2=55°.
∵∠DFB是△ABF的外角,∠B=25°,
∴∠DFB=∠BAF+∠B=∠CAD+∠BAC+∠B=10°+55°+25°=90°.
∵∠D=25°,
∴∠DGB=90°-25°=65°.

练习册系列答案
相关题目



