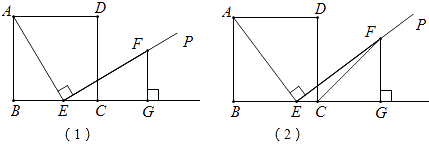��Ŀ����
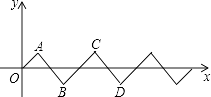
����Ŀ���Ƴ�ʫ��������ʫ���ŴӾ��С���ͷ����˵�������յ�ɽ����𣬻ƻ����������ӣ���ʫ��������һ����Ȥ����ѧ�������dz�֮Ϊ���������⡱����ͼ1��ʾ��ʫ�н����ڹ������֮���ɽ���µ�A��������ߵ����Աߵ�C���������ٵ�B����Ӫ�����������߲���ʹ�ܵ�·����̣�ij��������̽����һ����ʱ�������ѧģ�ͣ�
ֱ��lͬ������������A��B����ֱ��l�ϴ��ڵ�P��ʹ��PA+PB��ֵ��С��
�ⷨ������A����ֱ��l�ĶԳƵ�A�䣬����A��B����A��B��ֱ��l�Ľ��㼴ΪP����PA+PB����СֵΪ�߶�A��B�ij���
��1������������������ڱ���ͼ�л���������������⡱��ͼ�Σ�
��2��������Գ���ͼ������������⡱���������� ����
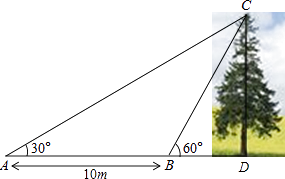
��3��Ӧ�ã�����ͼ2����֪��AOB=30�㣬���ڲ���һ��P��OP=12������AOB�����߷ֱ���C��D���㣨��ͬ�ڵ�O����ʹ��PCD���ܳ���С���뻭����ͼ���������PCD�ܳ�����Сֵ��
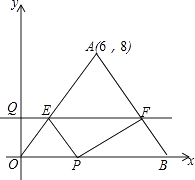
����ͼ3����A��4��2������B��1��6���ڵ�һ���ޣ���x�ᡢy�����Ƿ���ڵ�D����C��ʹ���ı���ABCD���ܳ���С�������ڣ��뻭����ͼ����������С�ܳ����������ڣ���˵�����ɣ�
���𰸡���1�������������2������֮���߶���̣���3����PCD���ܳ�=12���ı���ABCD���ܳ�����СֵΪ![]() +5��
+5��
��������
(1) ���ͼ
(2) ����������֮���߶����;
(3) �ٷֱ���P����OA��OB�ĶԳƵ�M��N������MN����OA��OB��C��D�����PCD���ܳ���С���ɵá�MONΪ�ȱ������Σ��ɵá�PCD���ܳ���
�ڵ�A����x��ĶԳƵ�F������Ϊ��4����2������B����y��ĶԳƵ�E������Ϊ����1��6��������EF��x�ᡢy���ڵ�D����C�����ı���ABCD���ܳ���С��������ԳƵ����ʿ�֪��BC=BE��DA=DF���ɵ��ı���ABCD���ܳ�����Сֵ.
�⣺��1����ͼ��ʾ��
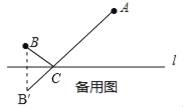
��2��
������Գ���ͼ������������⡱������������֮���߶���̣�
�ʴ�Ϊ������֮���߶���̣�
��3��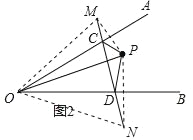
���ֱ���P����OA��OB�ĶԳƵ�M��N��
����MN����OA��OB��C��D������PCD���ܳ���С��
����OM��ON��
����ԳƵ����ʿ�֪��OM=OP=12��ON=OP=12��CP=CM��DP=DN��
��MON=2��AOB=60�㣬
���MONΪ�ȱ������Σ�
��MN=12��
���PCD���ܳ�=PC+CD+DC=CM+CD+DN=MN=12��
��
��A����x��ĶԳƵ�F������Ϊ��4����2������B����y��ĶԳƵ�E������Ϊ����1��6����
����EF��x�ᡢy���ڵ�D����C��
���ı���ABCD���ܳ���С��
������ԳƵ����ʿ�֪��BC=BE��DA=DF��
��BC+CD=AD=EC+CD+DF=EF=![]() =
=![]() ��
��
AB=![]() =5��
=5��
���ı���ABCD���ܳ�����СֵΪ![]() +5��
+5��

 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�