题目内容
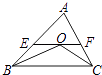
【题目】已知抛物线y1=ax2﹣4ax+3(a≠0)与y轴交于点A,A、B两点关于对称轴对称,直线OB分别与抛物线的对称轴相交于点C.
(1)直接写出对称轴及B点的坐标;
(2)已知直线y2=bx﹣4b+3(b≠0)与抛物线的对称轴相交于点D. ①判断直线y2=bx﹣4b+3(b≠0)是否经过点B,并说明理由;
②若△BDC的面积为1,求b的值.
【答案】
(1)解:∵抛物线为y1=ax2﹣4ax+3(a≠0),
∴对称轴是直线x=﹣ ![]() =2,
=2,
令x=0,则y=3,
∴A(0,3),
∵A、B两点关于对称轴对称,
∴B点的坐标为(4,3)
(2)解:①经过,
理由:把x=4代入直线y2=bx﹣4b+3(b≠0)点y2=3,
故直线y2=bx﹣4b+3(b≠0)是否经过点B;
②∵B(4,3),
∴直线OB为:y= ![]() x,
x,
把x=2代入得y= ![]() ,
,
∴C(2, ![]() ),
),
∵△BDC的面积为1,
∴ ![]() CD(4﹣2)=1,
CD(4﹣2)=1,
∴CD=1,
∴D(2, ![]() )或(2,
)或(2, ![]() ),
),
把(2, ![]() )代入y2=bx﹣4b+3得
)代入y2=bx﹣4b+3得 ![]() =2b﹣4b+3,
=2b﹣4b+3,
解得b= ![]() ;
;
把(2, ![]() )代入y2=bx﹣4b+3得
)代入y2=bx﹣4b+3得 ![]() =2b﹣4b+3,
=2b﹣4b+3,
解得b= ![]() ,
,
∴b的值为 ![]() 或
或 ![]()
【解析】(1)根据顶点公式即可求得对称轴,令x=0,求得A的坐标,然后根据轴对称的性质求得B的坐标;(2)①把B的坐标代入即可判断;②求得OB的解析式,即可求得C的坐标,根据C的坐标和三角形的面积即可求得D的坐标,然后根据待定系数法即可求得.

练习册系列答案
相关题目