题目内容
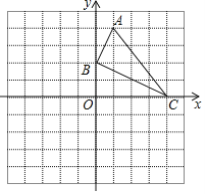
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(﹣2,6),C(2,2)两点.
(1)记抛物线顶点为D,求△BCD的面积;
(2)若直线y=﹣![]() x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.

【答案】(1)3 (2)![]() <b≤3.
<b≤3.
【解析】(1)根据待定系数法即可解决问题.求出直线BC与对称轴的交点H,根据S△BDC=S△BDH+S△DHC即可解决问题.
(2)由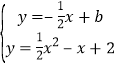 ,当方程组只有一组解时求出b的值,当直线y=﹣
,当方程组只有一组解时求出b的值,当直线y=﹣![]() x+b经过点C时,求出b的值,当直线y=﹣
x+b经过点C时,求出b的值,当直线y=﹣![]() x+b经过点B时,求出b的值,由此即可解决问题.
x+b经过点B时,求出b的值,由此即可解决问题.
解:(1)由题意![]() 解得
解得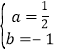 ,
,
∴抛物线解析式为y=![]() x2﹣x+2.
x2﹣x+2.
∵y=![]() x2﹣x+2=
x2﹣x+2=![]() (x﹣1)2+
(x﹣1)2+![]() .
.
∴顶点坐标(1,![]() ),
),
∵直线BC为y=﹣x+4,∴对称轴与BC的交点H(1,3),
∴S△BDC=S△BDH+S△DHC=![]() ×(3-
×(3-![]() )3+
)3+![]() ×(3-
×(3-![]() )1=3.
)1=3.
(2)由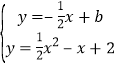 消去y得到x2﹣x+4﹣2b=0,
消去y得到x2﹣x+4﹣2b=0,
当△=0时,直线与抛物线相切,1﹣4(4﹣2b)=0,
∴b=![]() ,
,
当直线y=﹣![]() x+b经过点C时,b=3,
x+b经过点C时,b=3,
当直线y=﹣![]() x+b经过点B时,b=5,
x+b经过点B时,b=5,
∵直线y=﹣![]() x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,
x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,
∴![]() <b≤3.
<b≤3.
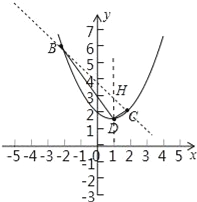
“点睛”本题考查待定系数法确定二次函数解析式、二次函数性质等知识,解题的关键是求出对称轴与直线BC交点H坐标,学会利用判别式确定两个函数图象的交点问题,属于中考常考题型.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目