题目内容
3.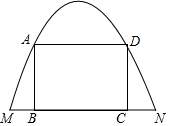 有一如图所示的纸片,拱形边缘呈抛物线形形状,MN=8米,抛物线顶点到边MN的距离是8米.点A和点D是抛物线上的两动点,且AD∥BC,过点A作AB⊥BC作DC⊥BC,过点B作DC⊥BC,点B、C在边MN上.
有一如图所示的纸片,拱形边缘呈抛物线形形状,MN=8米,抛物线顶点到边MN的距离是8米.点A和点D是抛物线上的两动点,且AD∥BC,过点A作AB⊥BC作DC⊥BC,过点B作DC⊥BC,点B、C在边MN上.(1)四边形ABCD是否可能为正方形?试说明明理由;
(2)试求四边形ABCD周长的最大值.
分析 (1)以MN所在直线为x轴、MN的中垂线为y轴建立平面直角坐标系,待定系数法求出函数解析式,设OC=a,则CD=-$\frac{1}{2}$a2+8,若四边形ABCD是正方形,由题意知四边形ABCD是矩形,则CD=2OC,据此列出关于a的方程,解之得出a的值,即可得答案;
(2)设矩形ABCD的周长为L,OC=a,则CD=-$\frac{1}{2}$a2+8,根据矩形的周长公式列出函数解析式并配方,从而由二次函数的性质可得答案.
解答 解:(1)能成为正方形,
如图,以MN所在直线为x轴、MN的中垂线为y轴建立平面直角坐标系,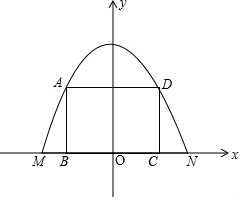
则该抛物线的顶点坐标为(0,8)、点M(-4,0)、N(4,0),
设解析式为y=ax2+8,
将点N(4,0)代入得:16a+8=0,
解得:a=-$\frac{1}{2}$,
∴y=-$\frac{1}{2}$x2+8,
∵AD∥BC,AB⊥BC,DC⊥BC,
∴四边形ABCD是矩形,
若四边形ABCD是正方形,
则CD=2OC,
设OC=a,则CD=-$\frac{1}{2}$a2+8,
∴-$\frac{1}{2}$a2+8=2a,
解得:a=-2-2$\sqrt{5}$<-4(舍),a=-2+2$\sqrt{5}$<4(符合题意),
故四边形ABCD可以是正方形.
(2)由(1)知,设矩形ABCD的周长为L,OC=a,则CD=-$\frac{1}{2}$a2+8,
∴L=4a+2(-$\frac{1}{2}$a2+8)=-a2+4a+16=-(a-2)2+20,
故当a=2时,L最大=20,
答:矩形ABCD的周长为20.
点评 本题主要考查二次函数的实际应用和正方形的判定,根据题意建立合适的平面直角坐标系并利用待定系数法求得函数解析式、根据正方形的判定得出关于a的方程和矩形周长公式列出函数解析式是解题的关键.

| A. | 3x-7 | B. | 2x-1=$\frac{1}{x}$ | C. | 4x-3=21x+17 | D. | x2-3=x |
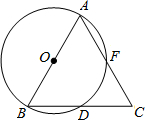 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.
如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.