��Ŀ����
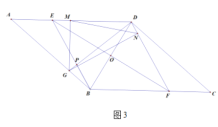
����Ŀ��һ����ֱ�Ĺ�·���м����������2400�ף�С�첽�дӼص��ҵأ�ÿ������100�ף�С���ﳵ���ҵص��غ���Ϣ2������ԭ·ԭ�ٷ����ҵأ�������ͬʱ�������˶���ʱ��Ϊt���֣������ҵصľ���Ϊs���ף���ͼ���߶�![]() ������
������![]() �ֱ��ʾ�������ҵؾ���s���˶�ʱ��t֮��ĺ�����ϵͼ��
�ֱ��ʾ�������ҵؾ���s���˶�ʱ��t֮��ĺ�����ϵͼ��

��1��С���ﳵ���ٶ�Ϊ__________��/���ӣ�
��2��B�������Ϊ__________��
��3��С�����ҵ�������ʱ��s��t֮��ĺ�������ʽΪ__________����д��t��ȡֵ��Χ��
��4��С���С������__________�ȵ����ҵأ��ȵ�__________���ӣ�
���𰸡�(1)200��/���ӣ�(2)(14,2400)��(3) s=200t(0��t��12)��(4)С�죬2����
��������
(1)����С���м���Ϣ��2���ӣ���Ӧ����ͼ��AB�Σ�������OABD��Ӧ����С���ĺ�����ϵͼ��EF��С���Ӧ�ĺ���ͼ����OA�μ������С���ﳵ�ٶȣ�
(2)��A��������2����B������꣬�������B�����ꣻ
(3)����ͼ��OA����������������Ӧ�Ľ���ʽ���ɣ�
(4)˭�õ�ʱ��̾ͱ�ʾ˭�ȴﵽ�ҵأ���ͼ�������.
�⣺(1)��ͼ��֪������OAED��ʾС�����˶�ͼ�Σ�EF��ʾС����˶�ͼ�Σ�
��С���ﳵ���ٶ�Ϊ��2400��12=200��/���ӣ�
�ʴ�Ϊ��200��/���ӣ�
(2)��ͼ��֪��A������Ϊ(12,2400),
��С������غ���Ϣ��2���ӣ�
��B������Ϊ(14,2400)��
�ʴ�Ϊ��(14,2400);
(3)С�����ҵص��أ���Ӧ����ͼ���߶�OA��
����OA����ֱ�ߵĽ���ʽΪ��s=kt
����A(12,2400),����2400=12k
���k=200��
��s��t֮��ĺ�������ʽΪ��s=200t(0��t��12)
�ʴ�Ϊ��s=200t(0��t��12).
(4)С����ͼ��F�㵽���ҵأ�С����ͼ��D�㵽���ҵأ�
��С���õ�ʱ����̣�
��С���ȵ����ҵ�
С����ٶ�Ϊÿ����100�ף�·��Ϊ2400��
��С�쵽���ҵ����õ�ʱ��Ϊ��2400��100=24���ӣ�
С��ȥʱ�ͻ�ʱ���ٶ���ͬ����Ϊ200��/���ӣ���·����ͬ��
��������е�ʱ���ȥʱ����ʱ����ͬ��Ϊ12���ӣ�
������;��Ϣ��2���ӣ���С��һ����ʱ��12+2+12=26���ӣ�
26-24=2��
��С���С���ȵ�2����.
�ʴ�Ϊ��С���ȵ��ҵأ��ȵ�2����.