题目内容
如图,AB⊥BC,DC⊥BC,垂足分别为B、C.(1)当AB=4,DC=1,BC=4时,在线段BC上是否点P,使AP⊥PD?如果存在求线段BP的长;如果不存在,请说明理由
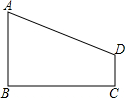 ;
;(2)设AB=a,DC=b,AD=c,那么当a、b、c之间满足什么关系时,在直线BC上存在点P,使AP⊥PD.
分析:(1)△ABP∽△PCD得出∠BPA+∠DPC=90°,即∠APD=90°,求出BP的长;
(2)过D作DE⊥AB于E,根据勾股定理用a、b、c表示出BC的长,再根据(1)的结论得出关于x的方程,利用一元二次方程跟的判别式即可求解.
(2)过D作DE⊥AB于E,根据勾股定理用a、b、c表示出BC的长,再根据(1)的结论得出关于x的方程,利用一元二次方程跟的判别式即可求解.
解答: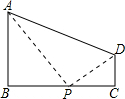 解:(1)存在.
解:(1)存在.
如图所示,AP⊥PD,
∴∠APD=90°,
∴∠APB+∠DPC=90°,
又∵DC⊥BC,
∴∠DCP=90°,
∴∠PDC+∠DPC=90°,
∴∠APB=∠PDC,
∵∠B=∠C,
∴△ABP∽△PCD,
设BP=x,则CP=4-x,
∴
=
,即4:(4-x)=x:1,
即x(4-x)=4,
∴x2-4x+4=0,
即(x-2)2=0,
得出x=2,即BP=2;
(2)过D作DE⊥AB于E,
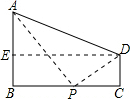 易得DC=BE=b,AE=a-b,BC=DE=
易得DC=BE=b,AE=a-b,BC=DE=
=
,
由(1)得△ABP∽△PCD,设PC=x,
则
=
,
化简得方程:x4-(c2-a2-b2)x2+a2b2=0,
若存在点P,则方程有实数根,
∴△=(c2-a2-b2)2-4a2b2=(c2-a2-b2+2ab)(c2-a2-b2-2ab)=[(c2-(a-b)2][c2-(a+b)2]≥0,
∵c>a-b,
∴c2-(a+b)2≥0,
∴c≥a+b,
∴当c≥a+b时,在直线BC上存在点P,使AP⊥PD.
 解:(1)存在.
解:(1)存在.如图所示,AP⊥PD,
∴∠APD=90°,
∴∠APB+∠DPC=90°,
又∵DC⊥BC,
∴∠DCP=90°,
∴∠PDC+∠DPC=90°,
∴∠APB=∠PDC,
∵∠B=∠C,
∴△ABP∽△PCD,
设BP=x,则CP=4-x,
∴
| AB |
| PC |
| BP |
| CD |
即x(4-x)=4,
∴x2-4x+4=0,
即(x-2)2=0,
得出x=2,即BP=2;
(2)过D作DE⊥AB于E,
 易得DC=BE=b,AE=a-b,BC=DE=
易得DC=BE=b,AE=a-b,BC=DE=| AD2-(AB-CD)2 |
| c2-(a-b)2 |
由(1)得△ABP∽△PCD,设PC=x,
则
| x |
| a |
| b | ||
|
化简得方程:x4-(c2-a2-b2)x2+a2b2=0,
若存在点P,则方程有实数根,
∴△=(c2-a2-b2)2-4a2b2=(c2-a2-b2+2ab)(c2-a2-b2-2ab)=[(c2-(a-b)2][c2-(a+b)2]≥0,
∵c>a-b,
∴c2-(a+b)2≥0,
∴c≥a+b,
∴当c≥a+b时,在直线BC上存在点P,使AP⊥PD.
点评:本题可以假设存在,根据相似三角形的性质得出比例式,找出P点.

练习册系列答案
相关题目
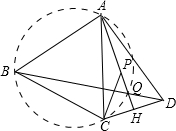 已知:如图,AB=BC=CA=AD,AH⊥CD于H,CP⊥BC,CP交AH于P.求证:△ABC的面积S=
已知:如图,AB=BC=CA=AD,AH⊥CD于H,CP⊥BC,CP交AH于P.求证:△ABC的面积S=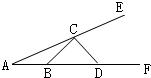 12、如图,AB=BC=CD,且∠A=15°,则∠ECD=( )
12、如图,AB=BC=CD,且∠A=15°,则∠ECD=( )
 如图,AB=BC=AC=AD,那么∠BDC等于( )
如图,AB=BC=AC=AD,那么∠BDC等于( )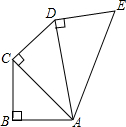 如图,AB=BC=CD=DE=1,且BC⊥AB,CD⊥AC,DE⊥AD,则线段AE的长为
如图,AB=BC=CD=DE=1,且BC⊥AB,CD⊥AC,DE⊥AD,则线段AE的长为