题目内容
 已知:如图,AB=BC=CA=AD,AH⊥CD于H,CP⊥BC,CP交AH于P.求证:△ABC的面积S=
已知:如图,AB=BC=CA=AD,AH⊥CD于H,CP⊥BC,CP交AH于P.求证:△ABC的面积S=
| ||
| 4 |
分析:因S△ABC=
BC2=
AC•BC,只须证AC•BC=AP•BD,转化为证△APC∽△BCD.这由A、B、C、Q四点共圆易证(Q为BD与AH交点).
| ||
| 4 |
| ||
| 4 |
解答: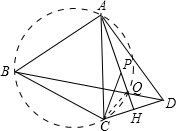 证明:记BD与AH交于点Q,则由AC=AD,AH⊥CD得∠ACQ=∠ADQ.
证明:记BD与AH交于点Q,则由AC=AD,AH⊥CD得∠ACQ=∠ADQ.
又AB=AD,故∠ADQ=∠ABQ.
从而∠ABQ=∠ACQ.可知A、B、C、Q四点共圆.
∵∠APC=90°+∠PCH=∠BCD,∠CBQ=∠CAQ,
∴△APC∽△BCD.
∴AC•BC=AP•BD.
于是,S=
AC•BC=
AP•BD.
 证明:记BD与AH交于点Q,则由AC=AD,AH⊥CD得∠ACQ=∠ADQ.
证明:记BD与AH交于点Q,则由AC=AD,AH⊥CD得∠ACQ=∠ADQ.又AB=AD,故∠ADQ=∠ABQ.
从而∠ABQ=∠ACQ.可知A、B、C、Q四点共圆.
∵∠APC=90°+∠PCH=∠BCD,∠CBQ=∠CAQ,
∴△APC∽△BCD.
∴AC•BC=AP•BD.
于是,S=
| ||
| 4 |
| ||
| 4 |
点评:本题考查了相似三角形的判定与性质及确定圆的条件,难度适中,关键是掌握相似三角形的判定方法.

练习册系列答案
相关题目
 8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( )
8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( ) 已知:如图,AB,CD相交于点O,且OA•OD=OB•OC,求证:AC∥DB.
已知:如图,AB,CD相交于点O,且OA•OD=OB•OC,求证:AC∥DB.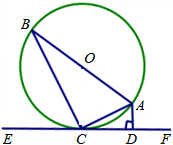 已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
 29、已知,如图,AB∥CD,∠EAB+∠FDC=180°.求证:AE∥FD.
29、已知,如图,AB∥CD,∠EAB+∠FDC=180°.求证:AE∥FD. 已知:如图,AB=AC,DB=DC,求证:∠B=∠C.
已知:如图,AB=AC,DB=DC,求证:∠B=∠C.