题目内容
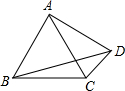如图，AB=BC=AC=AD，那么∠BDC等于（ ）分析：由AB=BC=AC=AD，可得点B，C，D在以A为圆心的圆上，△ABC是等边三角形，∠BAC的度数，又由在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半，即可求得答案．
解答：解：∵AB=BC=AC=AD，
∴点B，C，D在以A为圆心的圆上，△ABC是等边三角形，
∴∠BAC=60°，
∴∠BDC=
∠BAC=30°．
故选C．
∴点B，C，D在以A为圆心的圆上，△ABC是等边三角形，
∴∠BAC=60°，
∴∠BDC=
| 1 |
| 2 |
故选C．
点评：此题考查了圆周角定理以及等边三角形的判定与性质．此题难度适中，注意能得到点B，C，D在以A为圆心的圆上，△ABC是等边三角形是解此题的关键．
练习册系列答案
提分百分百检测卷系列答案
相关题目
已知：如图，AB=BC=CA=AD，AH⊥CD于H，CP⊥BC，CP交AH于P．求证：△ABC的面积S=
12、如图，AB=BC=CD，且∠A=15°，则∠ECD=（ ）
如图，AB=BC=CD=DE=1，且BC⊥AB，CD⊥AC，DE⊥AD，则线段AE的长为