题目内容
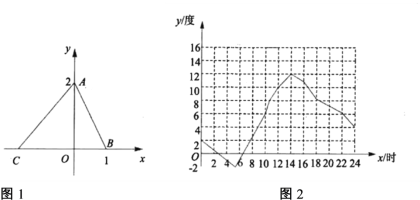
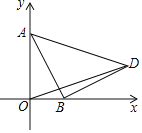
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为
为![]() 轴上一动点,以
轴上一动点,以![]() 为边在
为边在![]() 的右侧作等腰
的右侧作等腰![]() ,
,![]() ,连接
,连接![]() ,则
,则![]() 的最小值是 __________.
的最小值是 __________.
【答案】3![]() .
.
【解析】
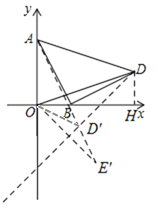
如图,作DH⊥x于H,利用全等三角形的判定与性质证明点D在直线y=x-3上运动,O关于直线y=x-3的对称点E′,连接AE′,求出AE′的长即可解决问题.
如图,作DH⊥x轴于H.
∵∠AOB=∠ABD=∠BHD=90°,
∴∠ABO+∠BAO=90°,∠ABO+∠DBH=90°,
∴∠BAO=∠DBH,
∵AB=DB,
∴△ABO≌△BDH(AAS),
∴OA=BH=3,OB=DH,
∴HD=OH-3,
∴点D在直线y=x-3上运动,
作O关于直线y=x-3的对称点E′,连接AE′交直线y=x-3于D′,
连接OD′,则OD′= D′E′
根据“两点之间,线段最短”可知此时OD+AD最小,最小值为AE′,
∵O(0,0),O关于直线y=x-3的对称点为E′,
∴E′(3,-3),
∵A(0,3),
∴AE′=3![]() ,
,
∴OD+AD的最小值是3![]() ,
,
故答案为:3![]() .
.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目