题目内容
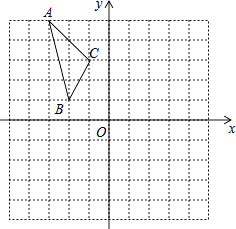
【题目】如图所示,在△ABC 中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于点E,交AC于点F.
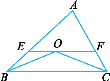
(1)若∠ABC=40°,∠ACB=60°,求∠BOE+∠COF的度数;
(2)若△AEF的周长为8 cm,且BC=4 cm,求△ABC的周长.
【答案】(1)∠BOE+∠COF=50°;(2)12cm.
【解析】
(1)两直线平行,内错角相等,以及根据角平分线性质,可得到![]() 从而求得∠BOE+∠COF的度数.
从而求得∠BOE+∠COF的度数.
(2)根据![]() ,可得△FOC、△EOB均为等腰三角形,由此把△AEF的周长转化为AC+AB,进而可得到△ABC的周长.
,可得△FOC、△EOB均为等腰三角形,由此把△AEF的周长转化为AC+AB,进而可得到△ABC的周长.
解:(1)∵EF∥BC,
∴∠OCB=∠COF,∠OBC=∠BOE.
又∵BO,CO分别是∠BAC和∠ACB的角平分线,
∴∠COF=∠FCO=![]() ∠ACB=30°,∠BOE=∠OBE=
∠ACB=30°,∠BOE=∠OBE=![]() ∠ABC=20°.
∠ABC=20°.
∴∠BOE+∠COF=50°.
(2)∵∠COF=∠FCO,∴OF=CF.
∵∠BOE=∠OBE,∴OE=BE.
∴△AEF的周长=AF+OF+OE+AE=AF+CF+BE+AE=AB+AC=8 cm.
∴△ABC的周长=8+4=12(cm).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目