题目内容
【题目】如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线l3上有点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上。
(1)如果点P在C、D之间运动时,试说明∠1+∠3=∠2;
(2)如果点P在直线l1的上方运动时,试探索∠1,∠2,∠3之间的关系又是如何?
(3)如果点P在直线l2的下方运动时,试探索∠PAC,∠PBD,∠APB之间的关系又是如何? (直接写出结论)

【答案】(1)证明见解析(2)当点P在线段DC的延长线上时,∠2=∠3-∠1(3)∠APB+∠PBD=∠PAC
【解析】分析:(1)过点P作PE∥l1,根据l1∥l2可知PE∥l2,根据平行线的性质可得出∠1=∠APE,∠3=∠BPE.再由∠2=∠APE+∠BPE即可得出结论;
(2)如图2所示,当点P在直线l1的上方运动时,∠2=∠3-∠1,过点P作PF∥l1,根据l1∥l2可知PE∥l2,根据平行线的性质可得出∠FPA=∠1,∠FPB=∠3, 即可得∠2=∠FPB-∠PFA=∠3-∠1;(3)∠APB+∠PBD=∠PAC,类比(2)的方法证明即可.
详解:
(1)证明:如图1,过点P作PE∥l1,
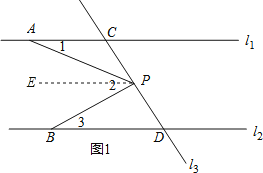
∵l1∥l2,
∴PE∥l2,
∴∠1=∠APE,∠3=∠BPE.
又∵∠2=∠APE+∠BPE,
∴∠2=∠1+∠3;
(2)如图2所示,当点P在直线l1的上方运动时,∠2=∠3-∠1.
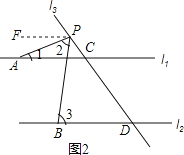
理由:过点P作PF∥l1,
∠FPA=∠1.
∵l1∥l2,
∴PF∥l2,
∴∠FPB=∠3,
∴∠2=∠FPB-∠PFA=∠3-∠1;
(3)∠APB+∠PBD=∠PAC,
理由:如图3所示,点P在直线l2的下方运动时,∠APB+∠PBD=∠PAC.
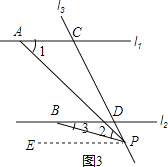
理由:过点P作PE∥l2,∠EPB=∠3.
∵l1∥l2,
∴PE∥l1,
∴∠EPA=∠1,
∴∠2=∠EPA-∠EPB=∠1-∠3.
即∠APB+∠PBD=∠PAC.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某市电力公司对全市用户采用分段计费的方式计算电费,收费标准如下表所示:
月用电量 | 不超过180度的部分 | 超过180度但不超过280度的部分 | 超过280度的部分 |
收费标准 | 0.5元/度 | 0.6元/度 | 0.9元/度 |
若某用户7月份的电费是139.2元,则该用户7月份用电为多少度?