题目内容
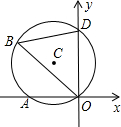 如图,⊙C通过原点并与坐标轴分别交于A、D两点,B是⊙C上一点,若∠OBD=60°,D点坐标为(3,0),则直线AD的解析式为________.
如图,⊙C通过原点并与坐标轴分别交于A、D两点,B是⊙C上一点,若∠OBD=60°,D点坐标为(3,0),则直线AD的解析式为________.
y= x+3
x+3
分析:连接AD,根据∠OBD=60°,得出∠OAD=60°,再根据tan∠OAD= ,OD=3,求出OA=
,OD=3,求出OA= ,得出A点坐标为(-
,得出A点坐标为(- ,0),最后代入直线AD的解析式为y=kx+b,解得:k=
,0),最后代入直线AD的解析式为y=kx+b,解得:k= ,即可得出直线AD的解析式.
,即可得出直线AD的解析式.
解答: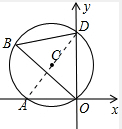 解:连接AD,
解:连接AD,
∵∠OBD=60°,
∴∠OAD=60°,
∵∠AOD=90°,
∴tan∠OAD= ,
,
∵D点坐标为(0,3),
∴OD=3,
∴tan60°=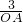 ,
,
∴OA= ,
,
∴A点坐标为(- ,0),
,0),
直线AD的解析式为y=kx+b,
则 ,
,
解得:k= ,
,
∴直线AD的解析式为y= x+3.
x+3.
故答案为:y= x+3.
x+3.
点评:本题考查了一次函数综合,用到的知识点是圆周角定理、解直角三角形、用待定系数法求一次函数的解析式,关键是求出点A的坐标.
 x+3
x+3分析:连接AD,根据∠OBD=60°,得出∠OAD=60°,再根据tan∠OAD=
 ,OD=3,求出OA=
,OD=3,求出OA= ,得出A点坐标为(-
,得出A点坐标为(- ,0),最后代入直线AD的解析式为y=kx+b,解得:k=
,0),最后代入直线AD的解析式为y=kx+b,解得:k= ,即可得出直线AD的解析式.
,即可得出直线AD的解析式.解答:
 解:连接AD,
解:连接AD,∵∠OBD=60°,
∴∠OAD=60°,
∵∠AOD=90°,
∴tan∠OAD=
 ,
,∵D点坐标为(0,3),
∴OD=3,
∴tan60°=
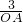 ,
,∴OA=
 ,
,∴A点坐标为(-
 ,0),
,0),直线AD的解析式为y=kx+b,
则
 ,
,解得:k=
 ,
,∴直线AD的解析式为y=
 x+3.
x+3.故答案为:y=
 x+3.
x+3.点评:本题考查了一次函数综合,用到的知识点是圆周角定理、解直角三角形、用待定系数法求一次函数的解析式,关键是求出点A的坐标.

练习册系列答案
相关题目
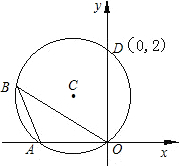 如图,⊙C通过原点,并与坐标轴分别交于A,D两点,已知∠OBA=30°,点D的坐标为(0,2),则点A,C的坐标分别为A(
如图,⊙C通过原点,并与坐标轴分别交于A,D两点,已知∠OBA=30°,点D的坐标为(0,2),则点A,C的坐标分别为A(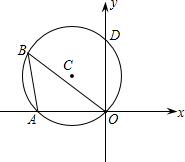 如图,⊙C通过原点,并与坐标轴分别交于A、D两点.已知∠OBA=30°,点D的坐标为(0,2),则点C的坐标为
如图,⊙C通过原点,并与坐标轴分别交于A、D两点.已知∠OBA=30°,点D的坐标为(0,2),则点C的坐标为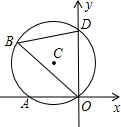 如图,⊙C通过原点并与坐标轴分别交于A、D两点,B是⊙C上一点,若∠OBD=60°,D点坐标为(3,0),则直线AD的解析式为
如图,⊙C通过原点并与坐标轴分别交于A、D两点,B是⊙C上一点,若∠OBD=60°,D点坐标为(3,0),则直线AD的解析式为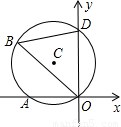 如图,⊙C通过原点并与坐标轴分别交于A、D两点,B是⊙C上一点,若∠OBD=60°,D点坐标为(3,0),则直线AD的解析式为 .
如图,⊙C通过原点并与坐标轴分别交于A、D两点,B是⊙C上一点,若∠OBD=60°,D点坐标为(3,0),则直线AD的解析式为 .