题目内容
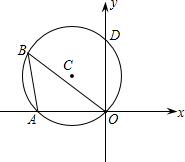如图，⊙C通过原点，并与坐标轴分别交于A、D两点．已知∠OBA=30°，点D的坐标为（0，2），则点C的坐标为分析：连接AD，则AD为直径，根据同弧所对的圆周角相等，可得出∠ADO=30°，再根据点D的坐标为（0，2），即可得出点C的坐标．
解答：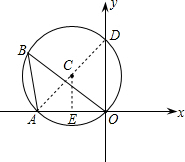
解：连接AD，过点C作CE⊥OA，
∴AD为直径，
∵∠OBA=30°，
∴∠ADO=30°，∠OAC=60°，
∴OA=
AD，OA=OC，
∵点D的坐标为（0，2），
∴OA2+OD2=AD2，
∴OA=
，
∴OE=
，
∴点C的坐标为（-
，1）．
解：连接AD，过点C作CE⊥OA，∴AD为直径，
∵∠OBA=30°，
∴∠ADO=30°，∠OAC=60°，
∴OA=
| 1 |
| 2 |
∵点D的坐标为（0，2），
∴OA2+OD2=AD2，
∴OA=
2
| ||
| 3 |
∴OE=
| ||
| 3 |
∴点C的坐标为（-
| ||
| 3 |
点评：本题考查了圆周角定理、坐标与图形的性质、解直角三角形，是基础知识要熟练掌握．
练习册系列答案
相关题目
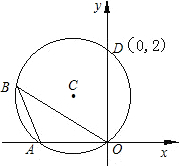如图，⊙C通过原点，并与坐标轴分别交于A，D两点，已知∠OBA=30°，点D的坐标为（0，2），则点A，C的坐标分别为A（
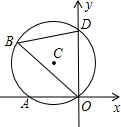如图，⊙C通过原点并与坐标轴分别交于A、D两点，B是⊙C上一点，若∠OBD=60°，D点坐标为（3，0），则直线AD的解析式为
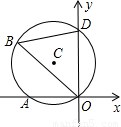如图，⊙C通过原点并与坐标轴分别交于A、D两点，B是⊙C上一点，若∠OBD=60°，D点坐标为（3，0），则直线AD的解析式为 ．