题目内容
(1)如图1,已知∠1=∠2,∠B=∠C,可推得AB∥CD,理由如下:
∵∠1=∠2(已知),
且∠1=∠CGD( ),
∴∠2=∠CGD(等量代换)
∴CE∥BF( )
∴∠ ECD =∠BFD( )
又∵∠B=∠C(已知)
∴∠BFD=∠B( )
∴AB∥CD( ).
(2)已知,如图2,AD∥BE,∠1=∠2,∠A与∠E相等吗?试说明理由.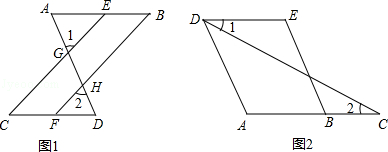
∵∠1=∠2(已知),
且∠1=∠CGD( ),
∴∠2=∠CGD(等量代换)
∴CE∥BF( )
∴∠ ECD =∠BFD( )
又∵∠B=∠C(已知)
∴∠BFD=∠B( )
∴AB∥CD( ).
(2)已知,如图2,AD∥BE,∠1=∠2,∠A与∠E相等吗?试说明理由.

(1)对顶角相等 同位角相等,两直线平行 两直线平行,同位角相等 等量代换 内错角相等,两直线平行
(2)相等,理由见解析
(2)相等,理由见解析
试题分析:(1)根据对顶角性质和已知推出∠2=∠CGD,推出CE∥BF,根据平行线的性质推出∠BFD=∠B即可;
(2)根据平行线的性质和判定推出∠A=∠EBC,∠E=∠EBC,即可得出答案.
解:(1)故答案为:对顶角相等,同位角相等,两直线平行,ECD,两直线平行,同位角相等,等量代换,内错角相等,两直线平行.
(2)相等,理由是:
∵∠1=∠2,
∴DE∥AC,
∴∠E=∠EBC,
∵AD∥BE,
∴∠A=∠EBC,
∴∠A=∠E.
点评:本题考查了平行线的性质和判定的应用,主要检查学生能否熟练地运用平行线的性质和判定进行推理和证明,题目比较典型.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 ,这个角是 度,这个角的补角是 度。
,这个角是 度,这个角的补角是 度。