题目内容
已知:在△ABC中,AD为∠BAC的平分线,以C为圆心,CD为半径的半圆交BC的延长线于点E,交AD于点F,交AE于点M,且∠B=∠CAE,FE:FD=4:3.(1)求证:AF=DF;
(2)求∠AED的余弦值;
(3)如果BD=10,求△ABC的面积.
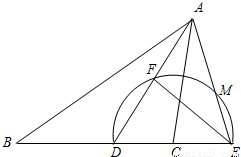
【答案】分析:(1)欲证AF=DF,可以证明△AEF≌△DEF得出;
(2)求∠AED的余弦值,即求ME:DM,由已知条件,勾股定理,切割线定理的推论可以求出;
(3)根据△ABC的面积公式求出BC,AN的长是关键,根据题意由三角函数及相似比即可求出.
解答:(1)证明:∵AD平分∠BAC
∴∠BAD=∠DAC
∵∠B=∠CAE
∴∠BAD+∠B=∠DAC+∠CAE
∵∠ADE=∠BAD+∠B
∴∠ADE=∠DAE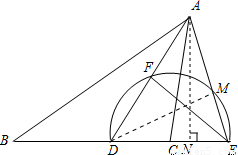
∴EA=ED
∵DE是半圆C的直径
∴∠DFE=90°
∴AF=DF(2分)
(2)解:连接DM
∵DE是半圆C的直径
∴∠DME=90°
∵FE:FD=4:3
∴可设FE=4x,则FD=3x
∴DE=5x
∴AE=DE=5x,AF=FD=3x
∵AF•AD=AM•AE
∴3x(3x+3x)=AM•5x
∴AM=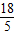 x
x
∴ME=AE-AM=5x-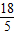 x=
x= x
x
在Rt△DME中,cos∠AED=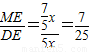 (5分)
(5分)
(3)解:过A点作AN⊥BE于N
∵cos∠AED=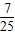
∴sin∠AED=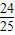
∴AN=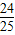 AE=
AE=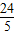 x
x
在△CAE和△ABE中
∵∠CAE=∠B,∠AEC=∠BEA
∴△CAE∽△ABE
∴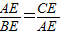
∴AE2=BE•CE
∴(5x)2=(10+5x)• x
x
∴x=2
∴AN=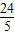 x=
x=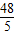
∴BC=BD+DC=10+ ×2=15
×2=15
∴S△ABC= BC•AN=
BC•AN= ×15×
×15×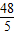 =72(8分).
=72(8分).
点评:本题考查相似三角形的判定,切割线定理,勾股定理,圆周角定理等知识点的综合运用.
(2)求∠AED的余弦值,即求ME:DM,由已知条件,勾股定理,切割线定理的推论可以求出;
(3)根据△ABC的面积公式求出BC,AN的长是关键,根据题意由三角函数及相似比即可求出.
解答:(1)证明:∵AD平分∠BAC
∴∠BAD=∠DAC
∵∠B=∠CAE
∴∠BAD+∠B=∠DAC+∠CAE
∵∠ADE=∠BAD+∠B
∴∠ADE=∠DAE

∴EA=ED
∵DE是半圆C的直径
∴∠DFE=90°
∴AF=DF(2分)
(2)解:连接DM
∵DE是半圆C的直径
∴∠DME=90°
∵FE:FD=4:3
∴可设FE=4x,则FD=3x
∴DE=5x
∴AE=DE=5x,AF=FD=3x
∵AF•AD=AM•AE
∴3x(3x+3x)=AM•5x
∴AM=
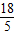 x
x∴ME=AE-AM=5x-
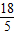 x=
x= x
x在Rt△DME中,cos∠AED=
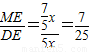 (5分)
(5分)(3)解:过A点作AN⊥BE于N
∵cos∠AED=
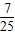
∴sin∠AED=
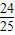
∴AN=
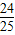 AE=
AE=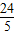 x
x在△CAE和△ABE中
∵∠CAE=∠B,∠AEC=∠BEA
∴△CAE∽△ABE
∴
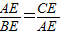
∴AE2=BE•CE
∴(5x)2=(10+5x)•
 x
x∴x=2
∴AN=
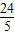 x=
x=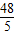
∴BC=BD+DC=10+
 ×2=15
×2=15∴S△ABC=
 BC•AN=
BC•AN= ×15×
×15×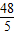 =72(8分).
=72(8分).点评:本题考查相似三角形的判定,切割线定理,勾股定理,圆周角定理等知识点的综合运用.

练习册系列答案
相关题目
 25、已知:在△ABC中AB=AC,点D在CB的延长线上.
25、已知:在△ABC中AB=AC,点D在CB的延长线上. (1)化简:(a-
(1)化简:(a- 20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长.
20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长. 12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
 已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.
已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.