题目内容
 如图,过反比例函数y=
如图,过反比例函数y=| 2 |
| x |
| A、S1>S2 |
| B、S1<S2 |
| C、S1=S2 |
| D、S1、S2的大小关系不能确定 |
分析:易得△AOC和△OBD的面积相等,都减去公共部分△OCE的面积可得S1、S2的大小关系.
解答:解:设点A的坐标为(x,y),点B的坐标为(a,b),
∵A、B在反比例函数y=
上,
∴xy=2,ab=2,
∴S△AOC=
xy=1;S△OBD=
ab=1.
∴S△AOC=S△OBD,
∴S△AOC-S△OCE=S△OBD-S△OCE,
即S1=S2.
故选C.
∵A、B在反比例函数y=
| 2 |
| x |
∴xy=2,ab=2,
∴S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△AOC=S△OBD,
∴S△AOC-S△OCE=S△OBD-S△OCE,
即S1=S2.
故选C.
点评:考查反比例函数的比例系数的意义;突破点是得到△AOC和△OBD的面积相等.用到的知识点为:在反比例函数图象上的点的横纵坐标的积等于反比例函数的比例系数.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
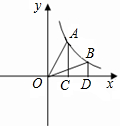 如图,过反比例函数y=
如图,过反比例函数y=| 9 |
| x |
| A、S1>S2 |
| B、S1=S2 |
| C、S1<S2 |
| D、大小关系不能确定 |
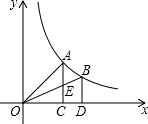 如图,过反比例函数y=
如图,过反比例函数y=| 1 |
| x |
| A、S1>S2 |
| B、S1=S2 |
| C、Sl<S2 |
| D、大小关系不能确定 |
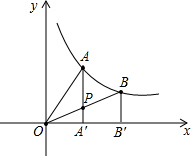 如图,过反比例函数y=
如图,过反比例函数y=| 2 |
| x |
| A、S1>S2 |
| B、S1=S2 |
| C、S1<S2 |
| D、大小关系不能确定 |
 如图,过反比例函数
如图,过反比例函数