题目内容
 如图,过反比例函数y=
如图,过反比例函数y=| 2 | x |
=
=
S2(填>、=或<)分析:根据反比例函数系数k的几何意义,可得△AOA′和△ROR′的面积相等,都减去公共部分△OA′P的面积可得S1、S2的大小关系.
解答:解:设点A的坐标为(xA,yA),点B的坐标为(xB,yB),
∵A、B在反比例函数数y=
(x>0)的图象上,
∴xAyA=2,xByB=2,
∴S△AOA′=
xAyA=1;S△ROR′=xByB=1.
∴S△AOA′=S△ROR′,
∴S△AOA′-S△OA′P=S△OBD-S△OA′P,
∴S△AOP=S梯形PA′B′B;
∴S1=S2.
故答案是:=.
∵A、B在反比例函数数y=
| 2 |
| x |
∴xAyA=2,xByB=2,
∴S△AOA′=
| 1 |
| 2 |
∴S△AOA′=S△ROR′,
∴S△AOA′-S△OA′P=S△OBD-S△OA′P,
∴S△AOP=S梯形PA′B′B;
∴S1=S2.
故答案是:=.
点评:本题考查了反比例函数系数k的几何意义:在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是
|k|,且保持不变.解答本题时采用了“数形结合”的数学思想.
| 1 |
| 2 |

练习册系列答案
相关题目
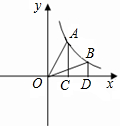 如图,过反比例函数y=
如图,过反比例函数y=| 9 |
| x |
| A、S1>S2 |
| B、S1=S2 |
| C、S1<S2 |
| D、大小关系不能确定 |
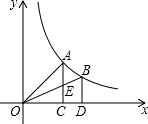 如图,过反比例函数y=
如图,过反比例函数y=| 1 |
| x |
| A、S1>S2 |
| B、S1=S2 |
| C、Sl<S2 |
| D、大小关系不能确定 |
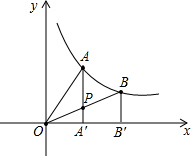 如图,过反比例函数y=
如图,过反比例函数y=| 2 |
| x |
| A、S1>S2 |
| B、S1=S2 |
| C、S1<S2 |
| D、大小关系不能确定 |
 如图,过反比例函数y=
如图,过反比例函数y=