题目内容
 如图,过反比例函数y=
如图,过反比例函数y=| 2 | x |
S1=S2
S1=S2
.分析:根据图形、三角形的面积公式(反比例函数系数k的几何意义)易得△AOC和△OBD的面积相等,都减去公共部分△OCE的面积可得S1、S2的大小关系.
解答:解:设点A的坐标为(xA,yA),点B的坐标为(xB,yB),
∵A、B在反比例函数y=
上,
∴xAyA=2,xByB=2,
∴S△AOC=
xAyA=1;S△OBD=
xByB=1.
∴S△AOC=S△OBD,
∴S△AOC-S△OCE=S△OBD-S△OCE,
∴S△AOE=S梯形ECDB;
又∵△AOE与梯形ECDB的面积分别为S1、S2,
∴S1=S2.
故答案是:S1=S2.
∵A、B在反比例函数y=
| 2 |
| x |
∴xAyA=2,xByB=2,
∴S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△AOC=S△OBD,
∴S△AOC-S△OCE=S△OBD-S△OCE,
∴S△AOE=S梯形ECDB;
又∵△AOE与梯形ECDB的面积分别为S1、S2,
∴S1=S2.
故答案是:S1=S2.
点评:本题考查了反比例函数系数k的几何意义.解答本题时采用了“数形结合”的数学思想.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
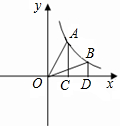 如图,过反比例函数y=
如图,过反比例函数y=| 9 |
| x |
| A、S1>S2 |
| B、S1=S2 |
| C、S1<S2 |
| D、大小关系不能确定 |
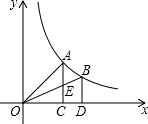 如图,过反比例函数y=
如图,过反比例函数y=| 1 |
| x |
| A、S1>S2 |
| B、S1=S2 |
| C、Sl<S2 |
| D、大小关系不能确定 |
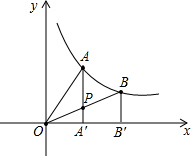 如图,过反比例函数y=
如图,过反比例函数y=| 2 |
| x |
| A、S1>S2 |
| B、S1=S2 |
| C、S1<S2 |
| D、大小关系不能确定 |
 如图,过反比例函数
如图,过反比例函数