ћвƒњƒЏ»Ё
°Њћвƒњ°њћљЊњ”лЈҐѕ÷:»зЌЉ1Ћщ ЊµƒЌЉ–ќ£ђѕсќ“√«≥£Љыµƒ—Іѕ∞”√∆Ј°™°™‘≤єж.ќ“√«≤їЈЅ∞—’в—щЌЉ–ќљ–„ц°∞єж–ќЌЉ°±£ђƒ«√і‘Џ’в“їЄцЉтµ•µƒЌЉ–ќ÷–£ђµљµ„“ю≤ЎЅЋƒƒ–© э—І÷™ ґƒЎ?ѕ¬√жЊЌ«лƒгЈҐї”ƒгµƒіѕ√ч≤≈÷«£ђљвЊц“‘ѕ¬ќ ћв:

(1)єџ≤м°∞єж–ќЌЉ°±£ђ ‘ћљЊњ![]() ”л
”л![]() ÷ЃЉдµƒєЎѕµ£ђ≤ҐЋµ√чјн”…;
÷ЃЉдµƒєЎѕµ£ђ≤ҐЋµ√чјн”…;
(2)«лƒг÷±љ”јы”√“‘…ѕљб¬џ£ђљвЊц“‘ѕ¬»эЄцќ ћв:
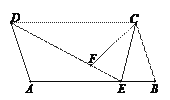
Ґў»зЌЉ2£ђ∞—“їњй»эљ«≥яXYZЈ≈÷√‘Џ![]() …ѕ£ђ є»эљ«≥яµƒЅљћх÷±љ«±яXY°ҐXZ«°Ї√Њ≠єэµгB°ҐC£ђ»ф
…ѕ£ђ є»эљ«≥яµƒЅљћх÷±љ«±яXY°ҐXZ«°Ї√Њ≠єэµгB°ҐC£ђ»ф![]() £ђ‘т
£ђ‘т![]() ________;
________;
ҐЏ»зЌЉ3£ђDC∆љЈ÷![]() £ђEC∆љЈ÷
£ђEC∆љЈ÷![]() £ђ»ф
£ђ»ф![]() £ђ«у
£ђ«у![]() µƒґ» э;
µƒґ» э;
Ґџ»зЌЉ4£ђ![]() µƒ10 µ»Ј÷ѕяѕаљї”Џµг
µƒ10 µ»Ј÷ѕяѕаљї”Џµг![]() £ђ»ф
£ђ»ф![]() £ђ«у°ѕAµƒґ» э.
£ђ«у°ѕAµƒґ» э.
°Њір∞Є°њ£®1£©°ѕBDC=°ѕA+°ѕB+°ѕC,јн”…Љыљвќц£ї£®2£©Ґў°ѕABX+°ѕACX=50°г£їҐЏ85°г£їҐџ63°г.
°Њљвќц°њ
£®1£© „ѕ»Ѕђљ”AD≤Ґ—”≥§÷ЅµгF£ђ»їЇуЄщЊЁ»эљ«–ќЌвљ«µƒ–‘÷ £ђЉіњ…≈–ґѕ≥ц°ѕBDC=°ѕA+°ѕB+°ѕC;
£®2£©Ґў”…£®1£©њ…µ√°ѕABX+°ѕACX+°ѕA=°ѕBXC£ђ»їЇуЄщЊЁ°ѕA=40°г£ђ°ѕBXC=90°г£ђ«у≥ц°ѕABX+°ѕACXµƒ÷µ «ґа…ўЉіњ…£Ѓ
ҐЏ”…£®1£©њ…µ√°ѕDBE=°ѕDAE+°ѕADB+°ѕAEB£ђ‘ўЄщЊЁ°ѕDAE=40°г£ђ°ѕDBE=130°г£ђ«у≥ц°ѕADB+°ѕAEBµƒ÷µ «ґа…ў£ї»їЇуЄщЊЁ°ѕDCE=![]() £®°ѕADB+°ѕAEB£©+°ѕDAE£ђ«у≥ц°ѕDCEµƒґ» э «ґа…ўЉіњ…£Ѓ
£®°ѕADB+°ѕAEB£©+°ѕDAE£ђ«у≥ц°ѕDCEµƒґ» э «ґа…ўЉіњ…£Ѓ
ҐџЄщЊЁ°ѕBG1C=![]() £®°ѕABD+°ѕACD£©+°ѕA£ђ°ѕBG1C=70°г£ђ…и°ѕAќ™x°г£ђњ…µ√°ѕABD+°ѕACD=133°г-x°г£ђљвЈљ≥ћ£ђ«у≥цxµƒ÷µ£ђЉіњ…≈–ґѕ≥ц°ѕAµƒґ» э «ґа…ў£Ѓ
£®°ѕABD+°ѕACD£©+°ѕA£ђ°ѕBG1C=70°г£ђ…и°ѕAќ™x°г£ђњ…µ√°ѕABD+°ѕACD=133°г-x°г£ђљвЈљ≥ћ£ђ«у≥цxµƒ÷µ£ђЉіњ…≈–ґѕ≥ц°ѕAµƒґ» э «ґа…ў£Ѓ
љв£Ї£®1£©»зЌЉ£®1£©£ђЅђљ”AD≤Ґ—”≥§÷ЅµгF£ђ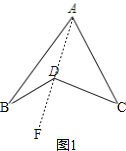 £ђ
£ђ
ЄщЊЁ»эљ«–ќЌвљ«µƒ–‘÷ £ђњ…µ√
°ѕBDF=°ѕBAD+°ѕB£ђ°ѕCDF=°ѕC+°ѕCAD£ђ
”÷°я°ѕBDC=°ѕBDF+°ѕCDF£ђ°ѕBAC=°ѕBAD+°ѕCAD£ђ
°а°ѕBDC=°ѕA+°ѕB+°ѕC£Ѓ
£®2£©Ґў”…£®1£©£ђњ…µ√
°ѕABX+°ѕACX+°ѕA=°ѕBXC£ђ
°я°ѕA=40°г£ђ°ѕBXC=90°г£ђ
°а°ѕABX+°ѕACX=90°г-40°г=50°г£Ѓ
ҐЏ”…£®1£©£ђњ…µ√
°ѕDBE=°ѕDAE+°ѕADB+°ѕAEB£ђ
°а°ѕADB+°ѕAEB=°ѕDBE-°ѕDAE=130°г-40°г=90°г£ђ
°а![]() £®°ѕADB+°ѕAEB£©=90°г°¬2=45°г£ђ
£®°ѕADB+°ѕAEB£©=90°г°¬2=45°г£ђ
°а°ѕDCE=![]() £®°ѕADB+°ѕAEB£©+°ѕDAE
£®°ѕADB+°ѕAEB£©+°ѕDAE
=45°г+40°г
=85°г£Ѓ
Ґџ°ѕBG1 C=![]() £®°ѕABD+°ѕACD£©+°ѕA£ђ
£®°ѕABD+°ѕACD£©+°ѕA£ђ
°я°ѕBG1 C=70°г£ђ
°а…и°ѕAќ™x°г£ђ
°я°ѕABD+°ѕACD=133°г-x°г
°а![]() £®133-x£©+x=70£ђ
£®133-x£©+x=70£ђ
°а13.3-![]() x+x=70£ђ
x+x=70£ђ
љвµ√x=63£ђЉі°ѕAµƒґ» эќ™63°г£Ѓ

 њ™–ƒЌ№њЏЋгћвњ®ѕµЅ–ір∞Є
њ™–ƒЌ№њЏЋгћвњ®ѕµЅ–ір∞Є°Њћвƒњ°њ…оџЏ –ƒ≥—І–£≥й—щµч≤й£ђAја—І…ъ∆пє≤ѕнµ•≥µ£ђBја—І…ъ„шєЂљї≥µ°ҐЋљЉ“≥µµ»£ђCја—І…ъ≤љ––£ђDја—І…ъ£®∆дЋь£©£ђЄщЊЁµч≤йљбєыїж÷∆ЅЋ≤їЌк’ыµƒЌ≥Љ∆ЌЉ£Ѓ
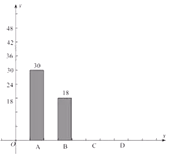
ја–Ќ | ∆µ э | ∆µ¬ |
A | 30 |
|
B | 18 | 0.15 |
C |
| 0.40 |
D |
|
|
£®1£©—І…ъє≤________»Ћ£ђ ![]() ________£ђ
________£ђ ![]() ________£ї
________£ї
£®2£©≤є»Ђћх–ќЌ≥Љ∆ЌЉ£ї
£®3£©»фЄ√–£є≤”–2000»Ћ£ђ∆пє≤ѕнµ•≥µµƒ”–________»Ћ£Ѓ