题目内容
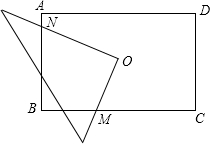 如图,O为矩形ABCD的中心,将直角三角板的直角顶点与O点重合,转动三角板使两直角边始终与BC,AB相交,交点分别为M,N.如果AB=4,AD=6,OM=x,ON=y.则y与x的关系是( )
如图,O为矩形ABCD的中心,将直角三角板的直角顶点与O点重合,转动三角板使两直角边始终与BC,AB相交,交点分别为M,N.如果AB=4,AD=6,OM=x,ON=y.则y与x的关系是( )A、y=
| ||
B、y=
| ||
| C、y=x | ||
D、y=
|
分析:根据矩形的性质,及相似三角形的性质得出y与x的关系.本题通过证明△OEN与△OFM相似得出.
解答: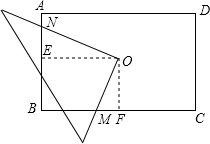 解:作OF⊥BC,OE⊥AB,则有∠OEN=∠OFM=90度.
解:作OF⊥BC,OE⊥AB,则有∠OEN=∠OFM=90度.
∵∠EOF=90度,
∴∠MOF=∠EOF-∠EOM=90°-∠EOM,
∵∠NOE=∠NOM-∠EOM=90°-∠EOM,
∴∠MOF=∠NOE,
∴△OEN与△OFM相似.
∴OE:OF=ON:OM,
∴
=
,
∴y=
x.
故选D.
 解:作OF⊥BC,OE⊥AB,则有∠OEN=∠OFM=90度.
解:作OF⊥BC,OE⊥AB,则有∠OEN=∠OFM=90度.∵∠EOF=90度,
∴∠MOF=∠EOF-∠EOM=90°-∠EOM,
∵∠NOE=∠NOM-∠EOM=90°-∠EOM,
∴∠MOF=∠NOE,
∴△OEN与△OFM相似.
∴OE:OF=ON:OM,
∴
| 3 |
| 2 |
| y |
| x |
∴y=
| 3 |
| 2 |
故选D.
点评:解决本题的关键是根据相似得到相应的等量关系.注意利用矩形的一些性质.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 26、如图,在等边△ABC中,点D是BC边的中点,以AD为边作等边△ADE.
26、如图,在等边△ABC中,点D是BC边的中点,以AD为边作等边△ADE.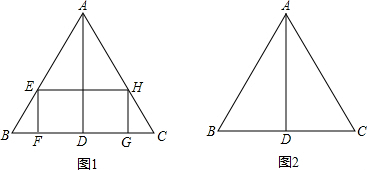


 如图,四边形DEFG是△ABC的内接矩形,如果△ABC的高线AH长8cm,底边BC长10cm,设DG=xcm,DE=ycm,则y关于x的函数关系式为
如图,四边形DEFG是△ABC的内接矩形,如果△ABC的高线AH长8cm,底边BC长10cm,设DG=xcm,DE=ycm,则y关于x的函数关系式为