题目内容
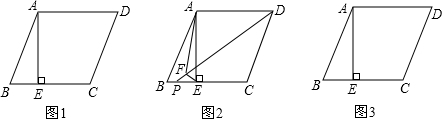
(1)如图1,在平行四边形ABCD中,E、F为BC上两点,且BE=CF,AF=DE.
求证:①△ABF≌△DCE;②四边形ABCD是矩形.
(2)如图2,已知△ABC是等边三角形,D点是AC的中点,延长BC到E,使CE=CD.
①请用尺规作图的方法,过点D作DM⊥BE,垂足为M;(不写作法,保留作图痕迹)
②求证:BM=EM.

求证:①△ABF≌△DCE;②四边形ABCD是矩形.
(2)如图2,已知△ABC是等边三角形,D点是AC的中点,延长BC到E,使CE=CD.
①请用尺规作图的方法,过点D作DM⊥BE,垂足为M;(不写作法,保留作图痕迹)
②求证:BM=EM.

分析:(1)①通过全等三角形的判定定理SSS证得△ABF≌△DCE,
②由①中的全等三角形得到对应角∠B=∠C,结合平行四边形的性质可以证得∠B=∠C=90°,故该平行四边形是矩形;
(2)①按照过直线外一点作已知直线的垂线步骤做;
②先根据D点AC的中点及等边三角形三线合一的性质得出∠ABD=∠CBD=
∠ABC=
∠ACB,由CE=CD可得出BD=DE,进而可得出△BDE是等腰三角形,由DM⊥BE即可得出结论.
②由①中的全等三角形得到对应角∠B=∠C,结合平行四边形的性质可以证得∠B=∠C=90°,故该平行四边形是矩形;
(2)①按照过直线外一点作已知直线的垂线步骤做;
②先根据D点AC的中点及等边三角形三线合一的性质得出∠ABD=∠CBD=
| 1 |
| 2 |
| 1 |
| 2 |
解答: (1)证明:①如图1,在平行四边形ABCD中,AB=CD.
(1)证明:①如图1,在平行四边形ABCD中,AB=CD.
∵BE=CF,
∴BF=CE,
∴在△ABF与△DCE中,
,
∴△ABF≌△DCE(SSS);
②由①知,△ABF≌△DCE,则∠B=∠C.
∵AB∥CD,
∴∠B+∠C=180°,
∴∠B=∠C=90°,
∴平行四边形ABCD是矩形;
(2)①如图2所示:
②如图2,∵△ABC是等边三角形,D点是AC的中点,
∴∠ABD=∠CBD=
∠ABC=
∠ACB,
又∵CE=CD,
∴∠E=∠CDE=
∠ACB,
∴∠E=∠CBD,
∴BD=DE
又∵DM⊥BE,
∴BM=EM.
 (1)证明:①如图1,在平行四边形ABCD中,AB=CD.
(1)证明:①如图1,在平行四边形ABCD中,AB=CD.∵BE=CF,
∴BF=CE,
∴在△ABF与△DCE中,
|
∴△ABF≌△DCE(SSS);
②由①知,△ABF≌△DCE,则∠B=∠C.
∵AB∥CD,
∴∠B+∠C=180°,
∴∠B=∠C=90°,
∴平行四边形ABCD是矩形;
(2)①如图2所示:
②如图2,∵△ABC是等边三角形,D点是AC的中点,
∴∠ABD=∠CBD=
| 1 |
| 2 |
| 1 |
| 2 |
又∵CE=CD,
∴∠E=∠CDE=
| 1 |
| 2 |
∴∠E=∠CBD,
∴BD=DE
又∵DM⊥BE,
∴BM=EM.
点评:本题考查的是全等三角形的判定与性质,矩形的判定以及等边三角形的性质,熟知等边三角形三线合一的性质是解答(2)题的关键.

练习册系列答案
相关题目
 如图1,在平行四边形ABCD中,AC=CD.
如图1,在平行四边形ABCD中,AC=CD.

