题目内容
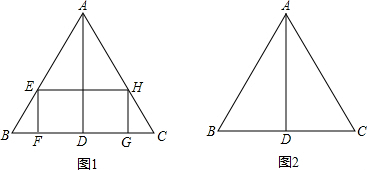
如图,等边三角形ABC,边长为2,AD是BC边上的高.(1)在△ABC内部作一个矩形EFGH(如图1),其中E、H分别在边AB、AC上,FG在边BC上.
①设矩形的一边FG=x,那么EF=
②设矩形的面积为y,当x取何值时,y的值最大,最大值是多少?
(2)在图2中,只用圆规画出点E,使得上述矩形EFGH面积最大.写出画法,并保留作图痕迹.
分析:(1)①FG=x,那么FD=
,易得BD=1,那么BF=1-
,∵∠B=60°,∠EFB=90°,∴EF=
-
x.
②面积=长×宽,那么就可以表示为关于x的二次函数,得出最值即可.
(2)由②得,FG=1时矩形面积最大,此时,BF=0.5,那么BE=1,那么以B为圆心,BD为半径画弧交AB于点E即可.
| x |
| 2 |
| x |
| 2 |
| 3 |
| ||
| 2 |
②面积=长×宽,那么就可以表示为关于x的二次函数,得出最值即可.
(2)由②得,FG=1时矩形面积最大,此时,BF=0.5,那么BE=1,那么以B为圆心,BD为半径画弧交AB于点E即可.
解答: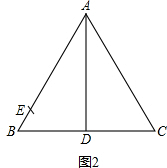 解:(1)①
解:(1)①
-
x.(2分)
②y=FG•EF=x(
-
x)=-
x2+
x(6分)
=-
(x-1)2+
.(7分)
当x=1时,y有最大值,且最大值为
.(8分)
(2)画法:以B为圆心,BD长为半径画弧,交AB于点E,则点E即为所求(10分)
画图正确(12分)
 解:(1)①
解:(1)①| 3 |
| ||
| 2 |
②y=FG•EF=x(
| 3 |
| ||
| 2 |
| ||
| 2 |
| 3 |
=-
| ||
| 2 |
| ||
| 2 |
当x=1时,y有最大值,且最大值为
| ||
| 2 |
(2)画法:以B为圆心,BD长为半径画弧,交AB于点E,则点E即为所求(10分)
画图正确(12分)
点评:解决本题的关键是根据等边三角形三线合一性质及特殊的三角函数求得矩形另一边长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知:如图,等边三角形AOB的顶点A在反比例函数y=
已知:如图,等边三角形AOB的顶点A在反比例函数y= 如图,等边三角形ABC中,D、E分别为AB、BC边上的两动点,且总使AD=BE,AE与CD交于点F,AG⊥CD于点G,则
如图,等边三角形ABC中,D、E分别为AB、BC边上的两动点,且总使AD=BE,AE与CD交于点F,AG⊥CD于点G,则 已知:如图,等边三角形ABC的边长为6,点D,E分别在边AB,AC上,且AD=AE=2.若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒.当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.
已知:如图,等边三角形ABC的边长为6,点D,E分别在边AB,AC上,且AD=AE=2.若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒.当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O. 如图,等边三角形ABC的边长为a,若D、E、F、G分别为AB、AC、CD、BF的中点,则△BEG的面积是( )
如图,等边三角形ABC的边长为a,若D、E、F、G分别为AB、AC、CD、BF的中点,则△BEG的面积是( )