题目内容
定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.(1)如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段
(2)在线段AC上确定一点P,使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上),请作出这个圆,并说明你的理由.友情提醒:“尺规作图”不要求写作法,但要保留作图痕迹.
(3)如图2,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连接BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由.若此时AB=3,BD=4
| 2 |


分析:(1)根据题中给出的定义,由于∠DAB和∠DCB不是直角,因此AC就是损矩形的直径.
(2)根据直角三角形斜边上中线的特点可知:此点应是AC的中点,那么可作AC的垂直平分线与AC的交点就是四边形外接圆的圆心.
(3)本题可用面积法来求解,具体思路是用四边形ABCD面积的不同表示方法来求解,四边形ABCD的面积=三角形ABD的面积+三角形BCD的面积=三角形ABC的面积+三角形ADC的面积;三角形ABD的面积已知了AB的长,那么可过D作AB边的高,那么这个高就应该是BD•sin45°,以此可得出三角形ABD的面积;三角形BDC的面积也可用同样的方法求解,只不过AB的长,换成了BC;再看三角形ABC的面积,已知了AB的长,可用含BC的式子表示出ABC的面积;而三角形ACD的面积,可用正方形面积的四分之一来表示;而正方形的边长可在直角三角形ABC中,用勾股定理求出.因此可得出关于BC的方程,求解即可得出BC的值.
(2)根据直角三角形斜边上中线的特点可知:此点应是AC的中点,那么可作AC的垂直平分线与AC的交点就是四边形外接圆的圆心.
(3)本题可用面积法来求解,具体思路是用四边形ABCD面积的不同表示方法来求解,四边形ABCD的面积=三角形ABD的面积+三角形BCD的面积=三角形ABC的面积+三角形ADC的面积;三角形ABD的面积已知了AB的长,那么可过D作AB边的高,那么这个高就应该是BD•sin45°,以此可得出三角形ABD的面积;三角形BDC的面积也可用同样的方法求解,只不过AB的长,换成了BC;再看三角形ABC的面积,已知了AB的长,可用含BC的式子表示出ABC的面积;而三角形ACD的面积,可用正方形面积的四分之一来表示;而正方形的边长可在直角三角形ABC中,用勾股定理求出.因此可得出关于BC的方程,求解即可得出BC的值.
解答: 解:(1)只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.因此AC是该损矩形的直径;
解:(1)只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.因此AC是该损矩形的直径;
(2)作图如图:
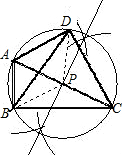
∵点P为AC中点,
∴PA=PC=
AC.
∵∠ABC=∠ADC=90°,
∴BP=DP=
AC,
∴PA=PB=PC=PD,
∴点A、B、C、D在以P为圆心,
AC为半径的同一个圆上;
(3)∵菱形ACEF,
∴∠ADC=90°,AE=2AD,CF=2CD,
∴四边形ABCD为损矩形,
∴由(2)可知,点A、B、C、D在同一个圆上.
∵BD平分∠ABC,
∴∠ABD=∠CBD=45°,
∴
=
,
∴AD=CD,
∴四边形ACEF为正方形.
∵BD平分∠ABC,BD=4
,
∴点D到AB、BC的距离h为4,
∴S△ABD=
AB×h=2AB=6,
S△ABC=
AB×BC=
BC,
S△BDC=
BC×h=2BC,S△ACD=
S正方形ACEF=
AC2=
(BC2+9),
∵S四边形ABCD=S△ABC+S△ADC=S△ABD+S△BCD
∴
BC+
(BC2+9)=6+2BC
∴BC=5或BC=-3(舍去),
∴BC=5.
 解:(1)只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.因此AC是该损矩形的直径;
解:(1)只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.因此AC是该损矩形的直径;(2)作图如图:

∵点P为AC中点,
∴PA=PC=
| 1 |
| 2 |
∵∠ABC=∠ADC=90°,
∴BP=DP=
| 1 |
| 2 |
∴PA=PB=PC=PD,
∴点A、B、C、D在以P为圆心,
| 1 |
| 2 |
(3)∵菱形ACEF,
∴∠ADC=90°,AE=2AD,CF=2CD,
∴四边形ABCD为损矩形,
∴由(2)可知,点A、B、C、D在同一个圆上.
∵BD平分∠ABC,
∴∠ABD=∠CBD=45°,
∴
 |
| AD |
 |
| CD |
∴AD=CD,
∴四边形ACEF为正方形.
∵BD平分∠ABC,BD=4
| 2 |
∴点D到AB、BC的距离h为4,
∴S△ABD=
| 1 |
| 2 |
S△ABC=
| 1 |
| 2 |
| 3 |
| 2 |
S△BDC=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
∵S四边形ABCD=S△ABC+S△ADC=S△ABD+S△BCD
∴
| 3 |
| 2 |
| 1 |
| 4 |
∴BC=5或BC=-3(舍去),
∴BC=5.
点评:本题主要考查了菱形的性质,正方形的判定,圆的内接四边形等知识点.(3)中如果无法直接求出线段的长,可通过特殊的三角形用面积法来求解.

练习册系列答案
相关题目
 标.
标. 21、定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.(1)如图,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段
21、定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.(1)如图,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段 如图,已知正方形ABCD的边长为1,点E是射线DA一动点(DE>1),连结BE,以BE为边在BE上方作正方形BEFG,设M为正方形BEFG的中心,如果定义:只有一组对角是直角的四边形叫做损矩形.
如图,已知正方形ABCD的边长为1,点E是射线DA一动点(DE>1),连结BE,以BE为边在BE上方作正方形BEFG,设M为正方形BEFG的中心,如果定义:只有一组对角是直角的四边形叫做损矩形. 轴正半轴上一动点(OD>1),连结BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交
轴正半轴上一动点(OD>1),连结BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交 轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形.
轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形.