题目内容
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:
销售量n(件) | n=50﹣x |
销售单价m(元/件) | m=20+ |
(1)请计算第几天该商品单价为25元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?
【答案】(1)第10天时该商品的销售单价为25元/件;(2)y=﹣![]() x2+15x+500;(3) 这30天中第15天获得的利润最大,最大利润是
x2+15x+500;(3) 这30天中第15天获得的利润最大,最大利润是![]() 元.
元.
【解析】
(1)将m=25代入m=20+![]() x,求得x即可;
x,求得x即可;
(2)根据“总利润=单件利润×销售量”可得函数解析式;
(3)将(2)中所得函数解析式配方成顶点式后,根据二次函数的性质即可得.
解:(1)当m=25时,20+![]() x=25,
x=25,
解得:x=10,
所以第10天时该商品的销售单价为25元/件;
(2)y=n(m﹣10)
=(50﹣x)(20+![]() x﹣10)
x﹣10)
=﹣![]() x2+15x+500;
x2+15x+500;
(3)y=﹣![]() x2+15x+500
x2+15x+500
=﹣![]() (x﹣15)2+
(x﹣15)2+![]() ,
,
∴当x=15时,y最大=![]() ,
,
答:这30天中第15天获得的利润最大,最大利润是![]() 元.
元.

【题目】某综合实践小组为了了解本校学生参加课外读书活动的情况,随机抽取部分学生,调查其最喜欢的图书类别,并根据调查结果绘制成如下不完整的统计表与统计图:
图书类别 | 画记 | 人数 | 百分比 | ||
文学类 | |||||
艺体类 | 正 | 5 | |||
科普类 | |||||
其他 | 正正 | 14 | |||
合计 | a | 100% |
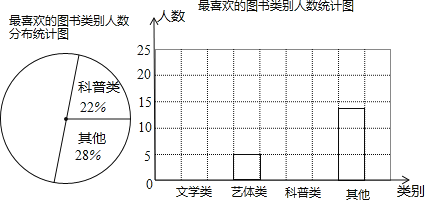
请结合图中的信息解答下列问题:
(1)随机抽取的样本容量![]() 为________;
为________;
(2)在扇形统计图中,“艺体类”所在的扇形圆心角应等于_________度;
(3)补全条形统计图;
(4)已知该校有![]() 名学生,估计全校最喜欢文学类图书的学生有________人.
名学生,估计全校最喜欢文学类图书的学生有________人.