题目内容
 如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点,
如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点,(1)求抛物线的解析式;
(2)求该抛物线的顶点坐标以及最值;
(3)已知AD=AB(D在线段AC上),有一动点P从点A沿线段AC以每秒1个单位长度的速度移动;同时另一个动点Q以某一速度从点B沿线段BC移动,经过t秒的移动,线段PQ被BD垂直平分,求t的值.
分析:(1)已知抛物线图象上的三点坐标,可利用待定系数法求出该抛物线的解析式;
(2)将(1)题所得抛物线的解析式,化为顶点坐标式,即可得到该抛物线的顶点坐标以及函数的最值;
(3)根据A、B的坐标,易求得AD=AB=5,则CD=AC-AD=2,连接DQ,由于BD垂直平分PQ,那么DP=DQ,根据等腰三角形三线合一的性质知:∠PDB=∠QDB=∠ABD,即AB∥DQ,此时△CDQ∽△CAB,利用相似三角形得到的比例线段即可求得DQ、PD的长,从而求得AP的值,进而可求得t的值.
(2)将(1)题所得抛物线的解析式,化为顶点坐标式,即可得到该抛物线的顶点坐标以及函数的最值;
(3)根据A、B的坐标,易求得AD=AB=5,则CD=AC-AD=2,连接DQ,由于BD垂直平分PQ,那么DP=DQ,根据等腰三角形三线合一的性质知:∠PDB=∠QDB=∠ABD,即AB∥DQ,此时△CDQ∽△CAB,利用相似三角形得到的比例线段即可求得DQ、PD的长,从而求得AP的值,进而可求得t的值.
解答: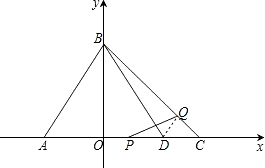 解:(1)设抛物线的解析式为:y=a(x+3)(x-4),则有:
解:(1)设抛物线的解析式为:y=a(x+3)(x-4),则有:
4=a(0+3)(0-4),a=-
;
故抛物线的解析式为:y=-
(x+3)(x-4)=-
x2+
x+4;
(2)由(1)知:y=-
x2+
x+4=-
(x-
)2+
,
故抛物线的顶点坐标为:(
,
),最大值为
;
(3)易知OA=3,OB=OC=4;
则AB=5,AC=7,CD=2;
连接DQ,由于BD垂直平分PQ,则DP=DQ,得:
∠PDB=∠QDB,
而AD=AB,得:∠ABD=∠ADB,
故∠QDB=∠ABD,
得QD∥AB;
∴△CDQ∽△CAB,则有:
=
,
=
,
∴PD=DQ=
,AP=AD-PD=5-
=
,
故t=
.
 解:(1)设抛物线的解析式为:y=a(x+3)(x-4),则有:
解:(1)设抛物线的解析式为:y=a(x+3)(x-4),则有:4=a(0+3)(0-4),a=-
| 1 |
| 3 |
故抛物线的解析式为:y=-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(2)由(1)知:y=-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 49 |
| 12 |
故抛物线的顶点坐标为:(
| 1 |
| 2 |
| 49 |
| 12 |
| 49 |
| 12 |
(3)易知OA=3,OB=OC=4;
则AB=5,AC=7,CD=2;
连接DQ,由于BD垂直平分PQ,则DP=DQ,得:
∠PDB=∠QDB,
而AD=AB,得:∠ABD=∠ADB,
故∠QDB=∠ABD,
得QD∥AB;
∴△CDQ∽△CAB,则有:
| CD |
| CA |
| DQ |
| AB |
| 2 |
| 7 |
| DQ |
| 5 |
∴PD=DQ=
| 10 |
| 7 |
| 10 |
| 7 |
| 25 |
| 7 |
故t=
| 25 |
| 7 |
点评:此题主要考查了二次函数解析式的确定、抛物线顶点坐标的求法、线段垂直平分线的性质、相似三角形的判定和性质等重要知识,难度适中.

练习册系列答案
相关题目
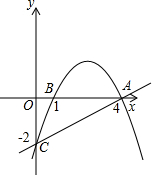 如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.
如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点. (2013•苏州一模)如图,抛物线经过A,C,D三点,且三点坐标为A(-1,0),C(0,5),D(2,5),抛物线与x轴的另一个交点为B点,点F为y轴上一动点,作平行四边形DFBG,
(2013•苏州一模)如图,抛物线经过A,C,D三点,且三点坐标为A(-1,0),C(0,5),D(2,5),抛物线与x轴的另一个交点为B点,点F为y轴上一动点,作平行四边形DFBG, (2013•高要市二模)已知:如图,抛物线经过点O、A、B三点,四边形OABC是直角梯形,其中点A在x轴上,点C在y轴上,BC∥OA,A(12,0)、B(4,8).
(2013•高要市二模)已知:如图,抛物线经过点O、A、B三点,四边形OABC是直角梯形,其中点A在x轴上,点C在y轴上,BC∥OA,A(12,0)、B(4,8).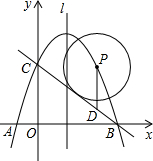 如图,抛物线经过A(-2,0)、B(8,0)两点,与y轴正半轴交与点C,且AB=BC,点P为第一象限内抛物线上一动点(不与B、C重合),设点P的坐标为(m,n).
如图,抛物线经过A(-2,0)、B(8,0)两点,与y轴正半轴交与点C,且AB=BC,点P为第一象限内抛物线上一动点(不与B、C重合),设点P的坐标为(m,n).