题目内容
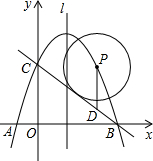 如图,抛物线经过A(-2,0)、B(8,0)两点,与y轴正半轴交与点C,且AB=BC,点P为第一象限内抛物线上一动点(不与B、C重合),设点P的坐标为(m,n).
如图,抛物线经过A(-2,0)、B(8,0)两点,与y轴正半轴交与点C,且AB=BC,点P为第一象限内抛物线上一动点(不与B、C重合),设点P的坐标为(m,n).(1)求抛物线的解析式;
(2)点D在BC上,且PD∥y轴,探索
| BD•DC | PD |
(3)设抛物线的对称轴为l,若以点P为圆心的⊙P与直线BC相切,请写出⊙P的半径R关于m函数关系式,并判断⊙P与直线l的位置关系.
分析:(1)AB=BC得C(0,6),设抛物线的交点式,利用待定系数法即可求得抛物线的解析式;
(2)设直线BC的解析式为y=kx+b,利用待定系数法即可求得直线BC的解析式,再根据两点间的距离公式可求PD=(-
m2+
m+6)-(-
m+6)=
m(8-m),CD=
m,BD=
(8-m).从而得到
的值;
(3)R=
PD=-
m(8-m),对称轴l:x=3.分若⊙P与l右切;若⊙P与l左切,可求m的值;再分当0<m<
或
<m<8时;当m=
或m=
时;当
<m<
时;三种情况讨论可得⊙P与直线l的位置关系.
(2)设直线BC的解析式为y=kx+b,利用待定系数法即可求得直线BC的解析式,再根据两点间的距离公式可求PD=(-
| 3 |
| 8 |
| 9 |
| 4 |
| 3 |
| 4 |
| 3 |
| 8 |
| 5 |
| 4 |
| 5 |
| 4 |
| BD•DC |
| PD |
(3)R=
| 4 |
| 5 |
| 3 |
| 10 |
17-
| ||
| 3 |
7+
| ||
| 3 |
17-
| ||
| 3 |
7+
| ||
| 3 |
17-
| ||
| 3 |
7+
| ||
| 3 |
解答:解:(1)由AB=BC得C(0,6).
设抛物线解析式为y=a(x+2)(x-8),则a=-
.
故y=-
(x+2)(x-8)=-
x2+
x+6;
(2)设直线BC的解析式为y=kx+b,将B(8,0),C(0,6)代入得
,
解得
.
故直线BC的解析式为y=-
x+6.
所以PD=(-
m2+
m+6)-(-
m+6)=
m(8-m),CD=
m,BD=
(8-m).所以
=
.
(3)R=
PD=-
m(8-m),对称轴l:x=3.
若⊙P与l右切,则-
(m2-8m)=m-3,解得m1=
(舍),m2=
;
若⊙P与l左切,则-
(m2-8m)=3-m,解得m1=
(舍),m2=
.
由于0<m<8,
所以,当0<m<
或
<m<8时,⊙P与直线l相离;
当m=
或m=
时,⊙P与直线l相切;
当
<m<
时,⊙P与直线l相交.
设抛物线解析式为y=a(x+2)(x-8),则a=-
| 3 |
| 8 |
故y=-
| 3 |
| 8 |
| 3 |
| 8 |
| 9 |
| 4 |
(2)设直线BC的解析式为y=kx+b,将B(8,0),C(0,6)代入得
|
解得
|
故直线BC的解析式为y=-
| 3 |
| 4 |
所以PD=(-
| 3 |
| 8 |
| 9 |
| 4 |
| 3 |
| 4 |
| 3 |
| 8 |
| 5 |
| 4 |
| 5 |
| 4 |
| BD•DC |
| PD |
| 25 |
| 6 |
(3)R=
| 4 |
| 5 |
| 3 |
| 10 |
若⊙P与l右切,则-
| 3 |
| 10 |
7-
| ||
| 3 |
7+
| ||
| 3 |
若⊙P与l左切,则-
| 3 |
| 10 |
17+
| ||
| 3 |
17-
| ||
| 3 |
由于0<m<8,
所以,当0<m<
17-
| ||
| 3 |
7+
| ||
| 3 |
当m=
17-
| ||
| 3 |
7+
| ||
| 3 |
当
17-
| ||
| 3 |
7+
| ||
| 3 |
点评:考查了二次函数综合题,涉及的知识点有:勾股定理,待定系数法求抛物线的解析式,待定系数法求直线的解析式,两点间的距离公式,切线的性质,直线与圆的位置关系,分类思想的运用,综合性较强,有一定的难度.

练习册系列答案
相关题目
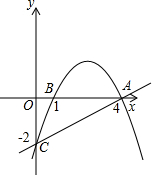 如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.
如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点. 如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点,
如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点, (2013•苏州一模)如图,抛物线经过A,C,D三点,且三点坐标为A(-1,0),C(0,5),D(2,5),抛物线与x轴的另一个交点为B点,点F为y轴上一动点,作平行四边形DFBG,
(2013•苏州一模)如图,抛物线经过A,C,D三点,且三点坐标为A(-1,0),C(0,5),D(2,5),抛物线与x轴的另一个交点为B点,点F为y轴上一动点,作平行四边形DFBG, (2013•高要市二模)已知:如图,抛物线经过点O、A、B三点,四边形OABC是直角梯形,其中点A在x轴上,点C在y轴上,BC∥OA,A(12,0)、B(4,8).
(2013•高要市二模)已知:如图,抛物线经过点O、A、B三点,四边形OABC是直角梯形,其中点A在x轴上,点C在y轴上,BC∥OA,A(12,0)、B(4,8).