题目内容
 (2013•高要市二模)已知:如图,抛物线经过点O、A、B三点,四边形OABC是直角梯形,其中点A在x轴上,点C在y轴上,BC∥OA,A(12,0)、B(4,8).
(2013•高要市二模)已知:如图,抛物线经过点O、A、B三点,四边形OABC是直角梯形,其中点A在x轴上,点C在y轴上,BC∥OA,A(12,0)、B(4,8).(1)求抛物线所对应的函数关系式;
(2)D为OA的中点,动点P自A点出发沿A→B→C→O的路线移动,若线段PD将梯形OABC的面积分成1﹕3两部分,求此时P点的坐标.
分析:(1)设所求抛物线的解析式为y=ax(x-12)+(a≠0),把A(12,0)、B(4,8)、C(0,0)三点代入即可求出a的值,进而得出该抛物线的解析式;
(2)过点B作BF⊥x轴于点F,先求出COAB的面积,由于点P的位置不能确定,故应分两种情况进行讨论:①当点P在AB上时,设点P的坐标为(x,y),由②当点P在OC上时,设点P的坐标为(0,y)求出满足题意的x和y的值即可得到P的坐标.
(2)过点B作BF⊥x轴于点F,先求出COAB的面积,由于点P的位置不能确定,故应分两种情况进行讨论:①当点P在AB上时,设点P的坐标为(x,y),由②当点P在OC上时,设点P的坐标为(0,y)求出满足题意的x和y的值即可得到P的坐标.
解答:(1)解:∵抛物线经过O(0,0)、A(12,0)、B(4,8),
∴设抛物线的解析式为:y=ax(x-12)…(1分)
∴将点B的坐标代入,得:8=4a(4-6),解得:a=-
,
∴所求抛物线的关系式为:y=-
x(x-12)=-
x2+3x;
(2)解:过点B作BF⊥x轴于点F,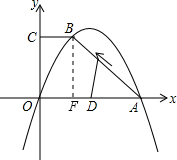
∵BF=8,AF=12-4=8
∴∠BAF=45°
∴S梯形OABC=
(4+12)×8=64,
∴面积分成1﹕3两部分,即面积分成16:48,
由题意得,动点P整个运动过程分三种情况,当点P在BC上时,
由于∵S△ABD=
×6×8=24 > 16
∴点P在BC上不能满足要求.
①点P在AB上,设P(x,y)
由S△APD=16,得
×AD×y=
×6×y=16
∴y=
…(6分)
过P作PE⊥x轴于点E,由∠BAF=45°
∴AE=PE=
,
∴x=12-
=
,
P(
,
)满足要求.
②点P在OC上,设P(0,y).
∵S△APD=
×AD×y=
×6×y=16
∴y=
,
∴P(0,
)满足要求.
∴设抛物线的解析式为:y=ax(x-12)…(1分)
∴将点B的坐标代入,得:8=4a(4-6),解得:a=-
| 1 |
| 4 |
∴所求抛物线的关系式为:y=-
| 1 |
| 4 |
| 1 |
| 4 |
(2)解:过点B作BF⊥x轴于点F,

∵BF=8,AF=12-4=8
∴∠BAF=45°
∴S梯形OABC=
| 1 |
| 2 |
∴面积分成1﹕3两部分,即面积分成16:48,
由题意得,动点P整个运动过程分三种情况,当点P在BC上时,
由于∵S△ABD=
| 1 |
| 2 |
∴点P在BC上不能满足要求.
①点P在AB上,设P(x,y)
由S△APD=16,得
| 1 |
| 2 |
| 1 |
| 2 |
∴y=
| 16 |
| 3 |
过P作PE⊥x轴于点E,由∠BAF=45°
∴AE=PE=
| 16 |
| 3 |
∴x=12-
| 16 |
| 3 |
| 20 |
| 3 |
P(
| 20 |
| 3 |
| 16 |
| 3 |
②点P在OC上,设P(0,y).
∵S△APD=
| 1 |
| 2 |
| 1 |
| 2 |
∴y=
| 16 |
| 3 |
∴P(0,
| 16 |
| 3 |
点评:本题考查的是二次函数综合题,此题涉及到用待定系数法求二次函数的解析式、梯形的面积公式及三角形的面积公式,根据题意作出辅助线,构造出三角形及梯形的高是解答此题的关键.

练习册系列答案
相关题目
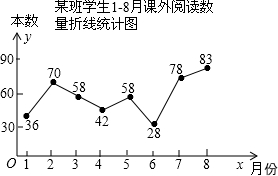 (2013•高要市二模)九(1)班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,阅读数量变化率最大的两个月是( )
(2013•高要市二模)九(1)班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,阅读数量变化率最大的两个月是( )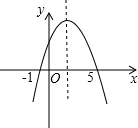 (2013•高要市二模)二次函数y=ax2+bx+c的部分图象如图所示,由图象可知该二次函数的图象的对称轴是直线x=
(2013•高要市二模)二次函数y=ax2+bx+c的部分图象如图所示,由图象可知该二次函数的图象的对称轴是直线x=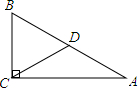 (2013•高要市二模)如图,在△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,连结CD.若AC=
(2013•高要市二模)如图,在△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,连结CD.若AC=