题目内容
某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: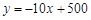 .
.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
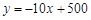 .
.(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
(1)当销售单价定为35元时,每月可获得最大利润;
(2)李明想要每月获得2000元的利润,销售单价应定为30元或40元;
(3)想要每月获得的利润不低于2000元,每月的成本最少为3600元.
(2)李明想要每月获得2000元的利润,销售单价应定为30元或40元;
(3)想要每月获得的利润不低于2000元,每月的成本最少为3600元.
试题分析:(1)由题意得,每月销售量与销售单价之间的关系可近似看作一次函数,利润=(定价﹣进价)×销售量,从而列出关系式;
(2)令w=2000,然后解一元二次方程,从而求出销售单价;
(3)根据抛物线的性质和图象,求出每月的成本.
试题解析:(1)由题意,得:w=(x﹣20)•y,
=(x﹣20)•(﹣10x+500)=﹣10x2+700x﹣10000,
x=
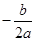 =35,
=35,答:当销售单价定为35元时,每月可获得最大利润;
(2)由题意,得:﹣10x2+700x﹣10000=2000,
解这个方程得:x1=30,x2=40,
答:李明想要每月获得2000元的利润,销售单价应定为30元或40元;
(3)∵a=﹣10<0,
∴抛物线开口向下,
∴当30≤x≤40时,w≥2000,
∵x≤32,
∴当30≤x≤32时,w≥2000,
设成本为P(元),由题意,得:P=20(﹣10x+500)=﹣200x+10000,
∵a=﹣200<0,
∴P随x的增大而减小,
∴当x=32时,P最小=3600,
答:想要每月获得的利润不低于2000元,每月的成本最少为3600元.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.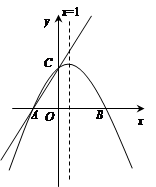
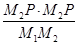 是否为定值,如果是,请直接写出结果,如果不是请说明理由.
是否为定值,如果是,请直接写出结果,如果不是请说明理由.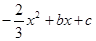 的图像经过B、C两点.
的图像经过B、C两点.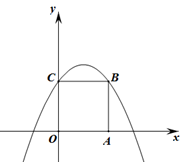
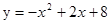 与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E.
与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E.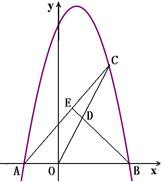
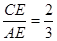 ;
;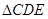 的面积为
的面积为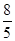 时,求
时,求 的值.
的值.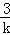 )与x轴交于点A、B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数是 _________ .
)与x轴交于点A、B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数是 _________ .