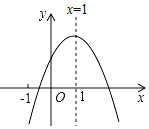��Ŀ����
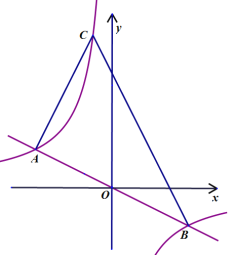
����Ŀ����֪A��B��C����˳����ͬһֱ���ϣ��ס������˾��ﳵ��A�س�������C��������ʻ���ױ��������5���ӣ�����B�ز���Ϣ��2���Ӻ������˼ף��ס���ͬʱ��B���Ը���ԭ�ټ�����C����ʻ�����ҵ���C�غ���������ͷ������Ϊԭ�ٵ�![]() ����ԭ·����A�أ�����Ҳ��������Ϊԭ�ٵ�
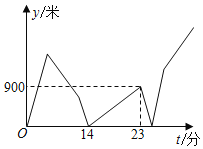
����ԭ·����A�أ�����Ҳ��������Ϊԭ�ٵ�![]() ��������C����ʻ������C�ؾ�ֹͣ�����ס��Ҽ�ľ���y���ף���׳�����ʱ��t���֣�֮��ĺ�����ϵ��ͼ��ʾ������C��ʱ���Ҿ�A��_____�ף�
��������C����ʻ������C�ؾ�ֹͣ�����ס��Ҽ�ľ���y���ף���׳�����ʱ��t���֣�֮��ĺ�����ϵ��ͼ��ʾ������C��ʱ���Ҿ�A��_____�ף�
���𰸡�6075��
��������
��������ͺ���ͼ���е����ݣ����Էֱ���ü��Ҹտ�ʼ���ٶȺͺ������ٶȣ�Ҳ�����A��B���صľ��롢A��C���صľ��룬Ȼ����ü���C��ʱ���Ҿ�A�ؾ��룮
�⣺������ɵã�
�������˸տ�ʼ���ٶ�֮��Ϊ��900�£�23��14����100����/�֣���
��տ�ʼ���ٶ�Ϊx��/�֣��Ҹտ�ʼ���ٶ�Ϊ��x+100����/�֣�
12x����14��5������x+100����
��ã�x��300��
��x+100��400��
��A��B����֮��ľ���Ϊ��300��12��3600���ף���
A��C����֮��ľ���Ϊ��400����23��5����7200���ף���
�ߵ��ҵ���C�غ���������ͷ������Ϊԭ�ٵ�![]() ����ԭ·����A�أ�����Ҳ��������Ϊԭ�ٵ�
����ԭ·����A�أ�����Ҳ��������Ϊԭ�ٵ�![]() ��������C����ʻ��
��������C����ʻ��
������ҵ��ٶ�Ϊ��400��![]() ��500����/�֣������ٶ�Ϊ300��
��500����/�֣������ٶ�Ϊ300��![]() ��400����/�֣���
��400����/�֣���
����C�ص�ʱ��Ϊ��23+[7200����23��2����300]��400��25![]() �����ӣ���
�����ӣ���
�൱����C��ʱ���Ҿ�A�أ�7200����25![]() ��23����500��6075���ף���
��23����500��6075���ף���
�ʴ�Ϊ��6075��


 ������ÿ�ʱ�Ż���ҵϵ�д�
������ÿ�ʱ�Ż���ҵϵ�д�