题目内容
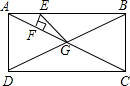 如图,已知点E是矩形ABCD的边AB上一点,且EF⊥AC,EG⊥BD,AB=4cm,AD=3cm,则EF+EG=
如图,已知点E是矩形ABCD的边AB上一点,且EF⊥AC,EG⊥BD,AB=4cm,AD=3cm,则EF+EG=分析:连接DE、CE,已知AB、AD,根据勾股定理即可求得BD的长,根据△BDE的面积、△AEC的面积之和即可求得EF+EG的值,即可解题.
解答: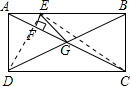 解:连接DE、CE,且BD=AC
解:连接DE、CE,且BD=AC
已知AB=4cm,AD=3cm,
∴BD=
=5cm,
则△BDE的面积=
BE•AD=
BD•EG,
△AEC的面积=
AE•BC=
AC•EF,
∴△BDE的面积与△AEC的面积之和=
AB•AD=
BD•(EF+EG)=
×3cm×4cm=6平方厘米,
∴EF+EG=
.
故答案为
.
 解:连接DE、CE,且BD=AC
解:连接DE、CE,且BD=AC已知AB=4cm,AD=3cm,
∴BD=
| AB2+AD2 |
则△BDE的面积=
| 1 |
| 2 |
| 1 |
| 2 |
△AEC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∴△BDE的面积与△AEC的面积之和=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴EF+EG=
| 12 |
| 5 |
故答案为
| 12 |
| 5 |
点评:本题考查了勾股定理在直角三角形中的运用,考查了三角形面积的计算,本题中根据△BDE的面积、△AEC的面积之和求EF+EG的值是解题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
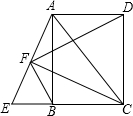 BF、FD.
BF、FD.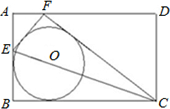 上翻折,若点B恰好在AD上,设这个点为F.
上翻折,若点B恰好在AD上,设这个点为F.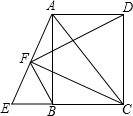 如图,已知点E是矩形ABCD的边CB延长线上一点,且CE=CA,连接AE,过点C作CF⊥AE,垂足为点F,连接BF、FD.
如图,已知点E是矩形ABCD的边CB延长线上一点,且CE=CA,连接AE,过点C作CF⊥AE,垂足为点F,连接BF、FD. ,且BD=10,求FC的值.
,且BD=10,求FC的值.