题目内容
如图,已知点E是矩形ABCD的边AB上一点,BE:EA=5:3,EC=15| 5 |
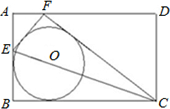 上翻折,若点B恰好在AD上,设这个点为F.
上翻折,若点B恰好在AD上,设这个点为F.(1)求AB、BC的长度各是多少?
(2)若⊙O内切于以F、E、B、C为顶点的四边形,求⊙O的面积.
分析:(1)求线段的长度问题,题中可先设其长度为k,然后利用三角形相似建立平衡关系,再用勾股定理求解即可.
(2)连接OB,由⊙O内切于以F、E、B、C为顶点的四边形,则BE=EF,BC=CF;再由BE:EA=5:3可以设BE=5x,EA=3x,则FA=4x,CD=8x,又CF=AD,CF2=CD2+DF2,可得CF=10x,DF=6x,则BC=10x;在Rt△EBC中,由勾股定理可求得x的值,再由面积S△EBC=S△OEB+S△OBC求得⊙O半径,求出面积.
(2)连接OB,由⊙O内切于以F、E、B、C为顶点的四边形,则BE=EF,BC=CF;再由BE:EA=5:3可以设BE=5x,EA=3x,则FA=4x,CD=8x,又CF=AD,CF2=CD2+DF2,可得CF=10x,DF=6x,则BC=10x;在Rt△EBC中,由勾股定理可求得x的值,再由面积S△EBC=S△OEB+S△OBC求得⊙O半径,求出面积.
解答:解:(1)∵四边形ABCD是矩形
∴∠A=∠B=∠D=90°,BC=AD,AB=CD,
∴∠AFE+∠AEF=90°(2分)
∵F在AD上,∠EFC=90°
∴∠AFE+∠DFC=90°
∴∠AEF=∠DFC
∴△AEF∽△DFC(3分)
∴
=
.(4分)
∵BE:EA=5:3
设BE=5k,AE=3k
∴AB=DC=8k,
由勾股定理得:AF=4k,
∴
=
∴DF=6k
∴BC=AD=10k(5分)
在△EBC中,根据勾股定理得BE2+BC2=EC2
∵CE=15
,BE=5k,BC=10k
∴(5k)2+(10k)2=(15
)2
∴k=3(6分)
∴AB=8k=24,BC=10k=30(7分)
(2)连接OB,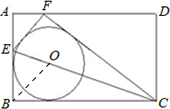
由于⊙O内切于以F、E、B、C为顶点的四边形,则BE=EF,BC=CF;
由BE:EA=5:3,设BE=5x,EA=3x,
则FA=4x,CD=8x,又CF=AD,∴CF2=CD2+DF2,即CF2=(8x)2+(CF-4x)2,可得CF=10x,DF=6x,则BC=10x;
在Rt△EBC中,EB2+BC2=EC2,即(5x)2+(10x)2=15
2,
解得:x=3,则BE=15,BC=30.
再由S△EBC=S△OEB+S△OBC,则
×BE×BC=
×BE×r+
×BC×r,
解得:r=10;
则⊙O的面积为πr2=100π.
∴∠A=∠B=∠D=90°,BC=AD,AB=CD,
∴∠AFE+∠AEF=90°(2分)
∵F在AD上,∠EFC=90°
∴∠AFE+∠DFC=90°
∴∠AEF=∠DFC
∴△AEF∽△DFC(3分)
∴
| AE |
| DF |
| AF |
| DC |
∵BE:EA=5:3
设BE=5k,AE=3k
∴AB=DC=8k,
由勾股定理得:AF=4k,
∴
| 3k |
| DF |
| 4k |
| 8k |
∴DF=6k
∴BC=AD=10k(5分)
在△EBC中,根据勾股定理得BE2+BC2=EC2
∵CE=15
| 5 |
∴(5k)2+(10k)2=(15
| 5 |
∴k=3(6分)
∴AB=8k=24,BC=10k=30(7分)
(2)连接OB,

由于⊙O内切于以F、E、B、C为顶点的四边形,则BE=EF,BC=CF;
由BE:EA=5:3,设BE=5x,EA=3x,
则FA=4x,CD=8x,又CF=AD,∴CF2=CD2+DF2,即CF2=(8x)2+(CF-4x)2,可得CF=10x,DF=6x,则BC=10x;
在Rt△EBC中,EB2+BC2=EC2,即(5x)2+(10x)2=15
| 5 |
解得:x=3,则BE=15,BC=30.
再由S△EBC=S△OEB+S△OBC,则
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:r=10;
则⊙O的面积为πr2=100π.
点评:本题考查了矩形的性质,会解决一些简单的翻折问题,能够利用勾股定理求解直角三角形;同时也考查了切线的性质及勾股定理的应用,难度稍大,解题时要理清思路.

练习册系列答案
相关题目
 BF、FD.
BF、FD.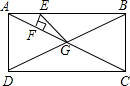 如图,已知点E是矩形ABCD的边AB上一点,且EF⊥AC,EG⊥BD,AB=4cm,AD=3cm,则EF+EG=
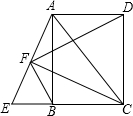
如图,已知点E是矩形ABCD的边AB上一点,且EF⊥AC,EG⊥BD,AB=4cm,AD=3cm,则EF+EG=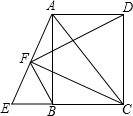 如图,已知点E是矩形ABCD的边CB延长线上一点,且CE=CA,连接AE,过点C作CF⊥AE,垂足为点F,连接BF、FD.
如图,已知点E是矩形ABCD的边CB延长线上一点,且CE=CA,连接AE,过点C作CF⊥AE,垂足为点F,连接BF、FD. ,且BD=10,求FC的值.
,且BD=10,求FC的值.