题目内容
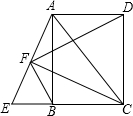 如图,已知点E是矩形ABCD的边CB延长线上一点,且CE=CA,连接AE,过点C作CF⊥AE,垂足为点F,连接BF、FD.
如图,已知点E是矩形ABCD的边CB延长线上一点,且CE=CA,连接AE,过点C作CF⊥AE,垂足为点F,连接BF、FD.(1)求证:△FBC≌△FAD;
(2)连接BD,若cos∠FBD=
| 3 | 5 |
分析:(1)根据等腰三角形三线合一的性质可得AF=EF,再根据直角三角形斜边上的中线等于斜边的一半可得BF=AF,然后利用等边对等角的性质得到∠FBA=∠FAB,从而推出∠FAD=∠FBC,再根据矩形的对边相等可得AD=BC,然后利用“边角边”即可证明;
(2)根据(1),利用全等三角形对应边相等可得FC=FD,全等三角形对应角相等可得∠BFC=∠AFD,然后证明∠BFD=90°,再根据余弦=
求出FB的长度,然后利用勾股定理列式计算即可求出FD,从而得解.
(2)根据(1),利用全等三角形对应边相等可得FC=FD,全等三角形对应角相等可得∠BFC=∠AFD,然后证明∠BFD=90°,再根据余弦=
| 邻边 |
| 斜边 |
解答:(1)证明:∵CE=AC,CF⊥AE,
∴AF=EF,
∴在Rt△ABE中,BF=AF,
∴∠FBA=∠FAB,
∵四边形ABCD是矩形,
∴AD=BC,∠ABC=∠BAD=90°,
∴∠FBA+∠ABC=∠FAB+∠BAD,
即∠FAD=∠FBC,
在△FBC和△FAD中,
∵
,
∴△FBC≌△FAD(SAS);
(2)解:∵△FBC≌△FAD,
∴FC=FD,∠BFC=∠AFD,
∴∠BFD=∠BFC+∠CFD=∠AFD+∠CFD=90°,
∵cos∠FBD=
=
,BD=10,
∴FB=
×10=6,
∴FD=
=
=8,
∴FC=8.
∴AF=EF,
∴在Rt△ABE中,BF=AF,
∴∠FBA=∠FAB,
∵四边形ABCD是矩形,
∴AD=BC,∠ABC=∠BAD=90°,
∴∠FBA+∠ABC=∠FAB+∠BAD,
即∠FAD=∠FBC,
在△FBC和△FAD中,
∵
|
∴△FBC≌△FAD(SAS);
(2)解:∵△FBC≌△FAD,
∴FC=FD,∠BFC=∠AFD,
∴∠BFD=∠BFC+∠CFD=∠AFD+∠CFD=90°,
∵cos∠FBD=
| FB |
| BD |
| 3 |
| 5 |
∴FB=
| 3 |
| 5 |
∴FD=
| BD2-FB2 |
| 102-62 |
∴FC=8.
点评:本题考查了矩形的性质,全等三角形的判定,等腰三角形三线合一的性质,直角三角形斜边上的中线等于斜边的一半的性质,以及锐角三角函数,综合性较强,但难度不大,求出∠FAD=∠FBC是证明三角形全等的关键,也是本题的难点.

练习册系列答案
相关题目
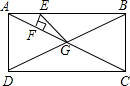 如图,已知点E是矩形ABCD的边AB上一点,且EF⊥AC,EG⊥BD,AB=4cm,AD=3cm,则EF+EG=
如图,已知点E是矩形ABCD的边AB上一点,且EF⊥AC,EG⊥BD,AB=4cm,AD=3cm,则EF+EG= 上翻折,若点B恰好在AD上,设这个点为F.
上翻折,若点B恰好在AD上,设这个点为F.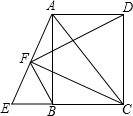 如图,已知点E是矩形ABCD的边CB延长线上一点,且CE=CA,连接AE,过点C作CF⊥AE,垂足为点F,连接BF、FD.
如图,已知点E是矩形ABCD的边CB延长线上一点,且CE=CA,连接AE,过点C作CF⊥AE,垂足为点F,连接BF、FD. ,且BD=10,求FC的值.
,且BD=10,求FC的值.