题目内容
如图,已知点E是矩形ABCD的边CB延长线上一点,且CE=CA,连接AE,过点C作CF⊥AE,垂足为点F,连接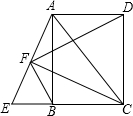 BF、FD.
BF、FD.(1)求证:△FBC≌△FAD;
(2)连接BD,若
| FB |
| BD |
| 3 |
| 5 |
分析:(1)根据CE=CA得到△ACE为等腰三角形,由CF⊥AE,根据“三线合一”得到F为AE的中点,又根据矩形的性质得到∠ABE为直角,在直角三角形ABE中,根据直角三角形斜边上的中线等于斜边的一半,即可得到AF等于BF,再根据等比对等角得到∠FAB=∠FBA,然后由∠BAD=∠ABC=90°,从而得到∠FAD=∠FBC,最后根据矩形的性质得到对边相等,AD=BC,根据“SAS”即可得证;
(2)根据(1)中的三角形全等得到FC=FD,且∠BFC=∠AFD,又∠AFC为直角,根据等量代换得到∠BFD为直角,由矩形的对角线相等,即AC=BD=10,根据已知的比例式可得FB的长,在直角三角形BFD中,利用勾股定理求出FD,即为FC的长.
(2)根据(1)中的三角形全等得到FC=FD,且∠BFC=∠AFD,又∠AFC为直角,根据等量代换得到∠BFD为直角,由矩形的对角线相等,即AC=BD=10,根据已知的比例式可得FB的长,在直角三角形BFD中,利用勾股定理求出FD,即为FC的长.
解答:(1)证明:∵CE=AC,CF⊥AE,∴AF=EF(1分)
∵四边形ABCD是矩形,
∴AD=BC,∠ABC=∠BAD=90°
∴在Rt△ABE中,BF=AF,(1分)
∴∠FBA=∠FAB,
∴∠FAD=∠FBC,(1分)
∴△FBC≌△FAD;(1分)
(2)解:∵△FBC≌△FAD,∴FC=FD,∠BFC=∠AFD(1分)
∴∠BFD=∠BFC+∠CFD=∠AFD+∠CFD=90°(1分)
∵四边形ABCD是矩形,∴BD=AC=10,
∵
=
,且BD=AC=10,∴FB=6,
在直角三角形BDF中,根据勾股定理得:FD=8,(1分)
∴FC=8.(1分)
∵四边形ABCD是矩形,
∴AD=BC,∠ABC=∠BAD=90°
∴在Rt△ABE中,BF=AF,(1分)
∴∠FBA=∠FAB,
∴∠FAD=∠FBC,(1分)
∴△FBC≌△FAD;(1分)
(2)解:∵△FBC≌△FAD,∴FC=FD,∠BFC=∠AFD(1分)
∴∠BFD=∠BFC+∠CFD=∠AFD+∠CFD=90°(1分)
∵四边形ABCD是矩形,∴BD=AC=10,
∵
| FB |
| BD |
| 3 |
| 5 |
在直角三角形BDF中,根据勾股定理得:FD=8,(1分)
∴FC=8.(1分)
点评:此题考查了矩形的性质,以及全等三角形的判别与性质.三角形全等的方法有:SAS,ASA,AAS,SSS及HL(直角三角形),注意根据题意选择合适的证明方法.第二问的思路是:利用第一问的结论得出相等的边及角,利用等量间的转换构造直角三角形,借助勾股定理解决问题.

练习册系列答案
相关题目
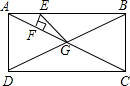 如图,已知点E是矩形ABCD的边AB上一点,且EF⊥AC,EG⊥BD,AB=4cm,AD=3cm,则EF+EG=
如图,已知点E是矩形ABCD的边AB上一点,且EF⊥AC,EG⊥BD,AB=4cm,AD=3cm,则EF+EG=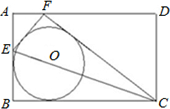 上翻折,若点B恰好在AD上,设这个点为F.
上翻折,若点B恰好在AD上,设这个点为F.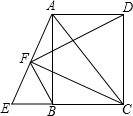 如图,已知点E是矩形ABCD的边CB延长线上一点,且CE=CA,连接AE,过点C作CF⊥AE,垂足为点F,连接BF、FD.
如图,已知点E是矩形ABCD的边CB延长线上一点,且CE=CA,连接AE,过点C作CF⊥AE,垂足为点F,连接BF、FD. ,且BD=10,求FC的值.
,且BD=10,求FC的值.