题目内容
【题目】已知:![]() 为⊙
为⊙![]() 的直径,
的直径,![]() ,弦
,弦![]() ,直线
,直线![]() 与
与![]() 相交于点
相交于点![]() ,弦
,弦![]() 在⊙
在⊙![]() 上运动且保持长度不变,⊙
上运动且保持长度不变,⊙![]() 的切线
的切线![]() 交
交![]() 于点
于点![]() .
.
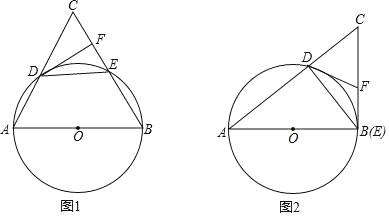
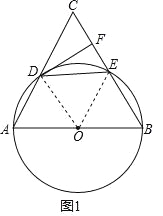
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
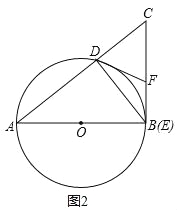
(2)如图2,当点![]() 运动至与点
运动至与点![]() 重合时,试判断
重合时,试判断![]() 与
与![]() 是否相等,并说明理由.
是否相等,并说明理由.
【答案】(1)证明见解析(2)相等
【解析】
试题分析:(1)如图1,连接OD、OE,证得△OAD、△ODE、△OEB、△CDE是等边三角形,进一步证得DF⊥CE即可证得结论;
(2)根据切线的性质以及等腰三角形的性质即可证得结论.
试题解析:(1)如图1,连接OD、OE,
∵AB=2,
∴OA=OD=OE=OB=1,
∵DE=1,
∴OD=OE=DE,
∴△ODE是等边三角形,
∴∠ODE=∠OED=60°,
∵DE∥AB,
∴∠AOD=∠ODE=60°,∠EOB=∠OED=60°,
∴△AOD和△△OE是等边三角形,
∴∠OAD=∠OBE=60°,
∴∠CDE=∠OAD=60°,∠CED=∠OBE=60°,
∴△CDE是等边三角形,
∵DF是⊙O的切线,
∴OD⊥DF,
∴∠EDF=90°﹣60°=30°,
∴∠DFE=90°,
∴DF⊥CE,
∴CF=EF;
(2)相等;
如图2,点E运动至与点B重合时,BC是⊙O的切线,
∵⊙O的切线DF交BC于点F,
∴BF=DF,
∴∠BDF=∠DBF,
∵AB是直径,
∴∠ADB=∠BDC=90°,
∴∠FDC=∠C,
∴DF=CF,
∴BF=CF.

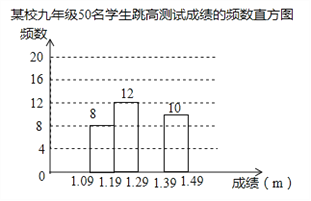
【题目】为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
某校九年级50名学生跳高测试成绩的频数表
组别(m) | 频数 |
1.09~1.19 | 8 |
1.19~1.29 | 12 |
1.29~1.39 | A |
1.39~1.49 | 10 |
(1)求a的值,并把频数直方图补充完整;
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.