题目内容
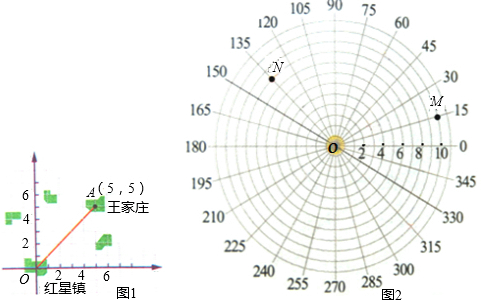
在向红星镇居民介绍王家庄位置的时候,我们可以这样说:如图1,在以红星镇为原点,正东方向为x轴正方向,正北方向为y轴正方向的平面直角坐标系(1单位长度表示的实际距离为1km)中,王家庄的坐标为(5,5);也可以说,王家庄在红星镇东北方向
km的地方.

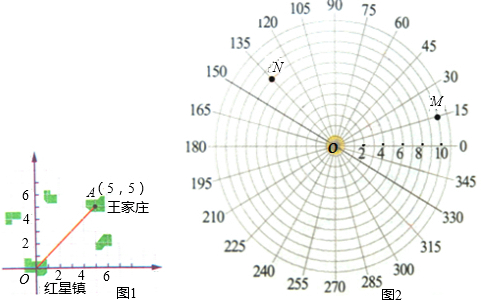
还有一种方法广泛应用于航海、航空、气象、军事等领域.如图2:在红星镇所建的雷达站O的雷达显示屏上,把周角每15°分成一份,正东方向为0°,相邻两圆之间的距离为1个单位长度(1单位长度表示的实际距离为1km),现发现2个目标,我们约定用(10,15°)表示点M在雷达显示器上的坐标,则:
(1)点N可表示为
(2)S△OMP=
(3)若有一家大型超市A在图中(4,30°)的地方,请直接标出点A,并将超市A与雷达站O连接,现准备在雷达站周围建立便民服务店B,使得△ABO为底角30°的等腰三角形,请直接写出B点在雷达显示屏上的坐标.
| 50 |

还有一种方法广泛应用于航海、航空、气象、军事等领域.如图2:在红星镇所建的雷达站O的雷达显示屏上,把周角每15°分成一份,正东方向为0°,相邻两圆之间的距离为1个单位长度(1单位长度表示的实际距离为1km),现发现2个目标,我们约定用(10,15°)表示点M在雷达显示器上的坐标,则:
(1)点N可表示为
(8,135°)
(8,135°)
;王家庄位置可表示为(
,45°)
| 50 |
(
,45°)
;点N关于雷达站点0成中心对称的点P的坐标为| 50 |
(8,315°)
(8,315°)
;(2)S△OMP=
20
| 2 |
20
;| 2 |
(3)若有一家大型超市A在图中(4,30°)的地方,请直接标出点A,并将超市A与雷达站O连接,现准备在雷达站周围建立便民服务店B,使得△ABO为底角30°的等腰三角形,请直接写出B点在雷达显示屏上的坐标.
(4,270°)或(4,150°)或(4
,0°)或(4
,60°).
| 3 |
| 3 |
(4,270°)或(4,150°)或(4
,0°)或(4
,60°).
.| 3 |
| 3 |
分析:(1)根据坐标中的第一个数值表示点到O的距离,第二个数表示这点于O的连线与正东方向形成的角度的大小,据此即可写出点的坐标;
(2)根据M、P的坐标可以求得OM=10,OP=8,∠MOP=45°,利用三角形的面积公式即可求解;
(3)根据(4,30°)表示的意义即可确定A的位置,讨论得到B的坐标.
(2)根据M、P的坐标可以求得OM=10,OP=8,∠MOP=45°,利用三角形的面积公式即可求解;
(3)根据(4,30°)表示的意义即可确定A的位置,讨论得到B的坐标.
解答:解:(1)答案是:( 8,135°),(
,45°),( 8,315°);
(2)OM=10,OP=8,∠MOP=45°,
则S△OMP=
OM•OP•sin45°=
×10×8×
=20
.
故答案是:20
;
(3)如图所示:
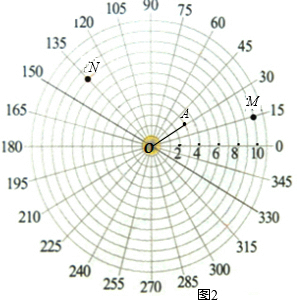
答案是:(4,270°)(4,150°)(4
,0°)( 4
,60°).
| 50 |
(2)OM=10,OP=8,∠MOP=45°,
则S△OMP=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 2 |
故答案是:20
| 2 |
(3)如图所示:

答案是:(4,270°)(4,150°)(4
| 3 |
| 3 |
点评:本题考查了点的坐标,以及三角形的面积公式,正确理解题意,理解坐标的意义是关键.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 km的地方。
km的地方。

 km的地方。
km的地方。

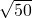 km的地方.
km的地方.